Dn represents the symmetry of a n dimensional polygon in a plane with rotation and reflection.
So if we let n = 3,4,5… we get:
- D3 = triangle
- D4 = square
- D5 = pentagon
- …
The group operation is composition.
general form of Cayley table:
| rotation |
reflection |
| reflection |
rotation |
Generators
<r , m | rn =1,r² = 1, m r m= r-1>
or equivalently:
<x , y | x² = y² = xyn = 1>
Combining Rotation and Reflection
As we have already seen that dihedral groups are not 'finite simple groups' which means that they must be the product of other types of group we also know that dihedral groups involve pure rotation (Cn) and pure reflection (C2). So how do we combine these two types of group to give a dihedral group? As we shall show below, the direct product does not produce the required result and we need to use the semidirect product defined as:
Dn Cn
Cn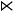 φ C2 where φ(0) = identity ,φ(1) = inversion
φ C2 where φ(0) = identity ,φ(1) = inversion
pure reflection C2
| generator |
cayley graph |
table |
| <m | m²> |
 |
|
pure rotation C3
| generator |
cayley graph |
table |
| <r | r³> |
 |
|
direct product C3 × C2
So lets try the direct product to see if that produces D3:
| generator |
cayley graph |
table |
| <m,r | m²,r³,rm=mr> |
 |
| {1,1} |
{r,1} |
{r²,1} |
{1,m} |
{r,m} |
{r²,m} |
| {r,1} |
{r²,1} |
{1,1} |
{r,m} |
{r²,m} |
{1,m} |
| {r²,1} |
{1,1} |
{r,1} |
{r²,m} |
{1,m} |
{r,m} |
| {1,m} |
{r,m} |
{r²,m} |
{1,1} |
{r,1} |
{r²,1} |
| {r,m} |
{r²,m} |
{1,m} |
{r,1} |
{r²,1} |
{1,1} |
| {r²,m} |
{1,m} |
{r,m} |
{r²,1} |
{1,1} |
{r,1} |
|
This is not what we want, reflection should reverse the rotation, so lets now try the semidirect product:
C3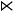 φ C2 where φ(0) = identity ,φ(1) = inversion
φ C2 where φ(0) = identity ,φ(1) = inversion
This produces the result that we expect:
| |
caley graph |
table |
| |
 |
| {1,1} |
{R,1} |
{R²,1} |
{1,m} |
{R,m} |
{R²,m} |
| {R,1} |
{R²,1} |
{1,1} |
{R,m} |
{R²,m} |
{1,m} |
| {R²,1} |
{1,1} |
{R,1} |
{R²,m} |
{1,m} |
{R,m} |
| {1,m} |
{R²,m} |
{R,m} |
{1,1} |
{R²,1} |
{R,1} |
| {R,m} |
{1,m} |
{R²,m} |
{R,1} |
{1,1} |
{R²,1} |
| {R²,m} |
{R,m} |
{1,m} |
{R²,1} |
{R,1} |
{1,1} |
|
Generating a Dihedral Group using a Program
We can use a computer program to generate these groups, here I have used Axiom/FriCAS which is described here.
(1) -> d1 := dihedralGroup(1)
<(1 2)>
Type: PermutationGroup(Integer)
(2) -> toTable()$toFiniteGroup(d1,1)
Type: Table(2)
(3) -> permutationRepresentation(d1,2)
Type: List(Matrix(Integer))
(4) -> d2 := dihedralGroup(2)
<(1 2),(3 4)>
Type: PermutationGroup(Integer)
(5) -> toTable()$toFiniteGroup(d2,1)
| i |
a |
b |
ab |
| a |
i |
ab |
b |
| b |
ab |
i |
a |
| ab |
b |
a |
i |
Type: Table(4)
(6) -> permutationRepresentation(d2,2)
Type: List(Matrix(Integer))
(7) -> d3 := dihedralGroup(3)
<(1 2 3),(1 3)>
Type: PermutationGroup(Integer)
(8) -> toTable()$toFiniteGroup(d3,1)
| i |
a |
b |
aa |
ab |
ba |
| a |
aa |
ab |
i |
ba |
b |
| b |
ba |
i |
ab |
aa |
a |
| aa |
i |
ba |
a |
b |
ab |
| ab |
b |
a |
ba |
i |
aa |
| ba |
ab |
aa |
b |
a |
i |
Type: Table(6)
(9) -> permutationRepresentation(d3,3)
Type: List(Matrix(Integer))
(10) -> d4 := dihedralGroup(4)
<(1 2 3 4),(1 4)(2 3)>
Type: PermutationGroup(Integer)
(11) -> toTable()$toFiniteGroup(d4,1)
| i |
a |
b |
aa |
ab |
ba |
aaa |
aab |
| a |
aa |
ab |
aaa |
aab |
b |
i |
ba |
| b |
ba |
i |
aab |
aaa |
a |
ab |
aa |
| aa |
aaa |
aab |
i |
ba |
ab |
a |
b |
| ab |
b |
a |
ba |
i |
aa |
aab |
aaa |
| ba |
aab |
aaa |
ab |
aa |
i |
b |
a |
| aaa |
i |
ba |
a |
b |
aab |
aa |
ab |
| aab |
ab |
aa |
b |
a |
aaa |
ba |
i |
Type: Table(8)
(12) -> permutationRepresentation(d4,4)
|
[
|
| 0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
|
,
|
| 0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 1 |
0 |
0 |
0 |
|
|
]
|
Type: List(Matrix(Integer))
(13) -> d5 := dihedralGroup(5)
<(1 2 3 4 5),(1 5)(2 4)>
Type: PermutationGroup(Integer)
(14) -> toTable()$toFiniteGroup(d5,1)
| i |
a |
b |
aa |
ab |
ba |
aaa |
aab |
baa |
bab |
| a |
aa |
ab |
aaa |
aab |
b |
bab |
baa |
ba |
i |
| b |
ba |
i |
baa |
bab |
a |
aab |
aaa |
aa |
ab |
| aa |
aaa |
aab |
bab |
baa |
ab |
i |
ba |
b |
a |
| ab |
b |
a |
ba |
i |
aa |
baa |
bab |
aaa |
aab |
| ba |
baa |
bab |
aab |
aaa |
i |
ab |
aa |
a |
b |
| aaa |
bab |
baa |
i |
ba |
aab |
a |
b |
ab |
aa |
| aab |
ab |
aa |
b |
a |
aaa |
ba |
i |
bab |
baa |
| baa |
aab |
aaa |
ab |
aa |
bab |
b |
a |
i |
ba |
| bab |
i |
ba |
a |
b |
baa |
aa |
ab |
aab |
aaa |
Type: Table(10)
(15) -> permutationRepresentation(d5,5)
|
[
|
| 0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
|
,
|
| 0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
|
|
]
|
Type: List(Matrix(Integer))
(16) -> d6 := dihedralGroup(6)
<(1 2 3 4 5 6),(1 6)(2 5)(3 4)>
Type: PermutationGroup(Integer)
(17) -> toTable()$toFiniteGroup(d6,1)
| i |
a |
b |
aa |
ab |
ba |
aaa |
aab |
baa |
bab |
aaaa |
aaab |
| a |
aa |
ab |
aaa |
aab |
b |
aaaa |
aaab |
ba |
i |
bab |
baa |
| b |
ba |
i |
baa |
bab |
a |
aaab |
aaaa |
aa |
ab |
aab |
aaa |
| aa |
aaa |
aab |
aaaa |
aaab |
ab |
bab |
baa |
b |
a |
i |
ba |
| ab |
b |
a |
ba |
i |
aa |
baa |
bab |
aaa |
aab |
aaab |
aaaa |
| ba |
baa |
bab |
aaab |
aaaa |
i |
aab |
aaa |
a |
b |
ab |
aa |
| aaa |
aaaa |
aaab |
bab |
baa |
aab |
i |
ba |
ab |
aa |
a |
b |
| aab |
ab |
aa |
b |
a |
aaa |
ba |
i |
aaaa |
aaab |
baa |
bab |
| baa |
aaab |
aaaa |
aab |
aaa |
bab |
ab |
aa |
i |
ba |
b |
a |
| bab |
i |
ba |
a |
b |
baa |
aa |
ab |
aaab |
aaaa |
aaa |
aab |
| aaaa |
bab |
baa |
i |
ba |
aaab |
a |
b |
aab |
aaa |
aa |
ab |
| aaab |
aab |
aaa |
ab |
aa |
aaaa |
b |
a |
bab |
baa |
ba |
i |
Type: Table(12)
(18) -> permutationRepresentation(d6,6)
|
[
|
| 0 |
0 |
0 |
0 |
0 |
1 |
| 1 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
0 |
1 |
0 |
|
,
|
| 0 |
0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
|
|
]
|
Type: List(Matrix(Integer))
|
where:
- The points of the permutation are numbered 1..n
- The elements of the group are named: "i" for the identity, single letters "a","b"... for the generators, and products of these.
- numbers in '<' '>' brackets are points of permutations represented in cyclic notation.
- The permutation is represented by a set of comma seperated permutations in angle brackets like this: <(1 2)(3 4),(1 2 3)>
- non-changing elements of the permutation are ommited so the above case is equivalent to: <(1 2)(3 4),(1 2 3)(4)>
- attempting to produce a dihedral group with less than 3 elements does not produce a valid result.
- The Axiom/FriCAS program can't work in terms of the Cayley table, so I have added my own code to do this.
![]() Cn
Cn![]() φ C2 where φ(0) = identity ,φ(1) = inversion
φ C2 where φ(0) = identity ,φ(1) = inversion 

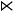 φ C2 where φ(0) = identity ,φ(1) = inversion
φ C2 where φ(0) = identity ,φ(1) = inversion 
