Physics - Energy and Momentum

Prerequisites

If you are not familiar with this subject you may like to look at the following pages first:

State vector for an unconstrained rigid body

In the pages about kinematics the position of an unconstrained rigid body was represented by 6 dimentional vector as follows:

θx angle about x
θy angle about y
θz angle about z
Px position of centre of mass along x axis
Py position of centre of mass along y axis
Pz position of centre of mass along z axis

When we are implementing a dynamics system we also need to include the objects momentum in its state vector, so we need 12 values as follows:

θx angle about x
θy angle about y
θz angle about z
Px position of centre of mass along x axis
Py position of centre of mass along y axis
Pz position of centre of mass along z axis
lx angular momentum about x
ly angular momentum about y
lz angular momentum about z
mvx momentum along x axis
mvy momentum along y axis
mvz momentum along z axis

Of course there are a lot of other parameters associated with each object, such as shape, colour and other physical properties such as coeficient of friction, but these are all reasonably constant. The above state vector holds the parameters which may be continously changing in a dynamics system with forces being applied

Conservation of Energy and Momentum

There are two quantities which are conserved, energy and momentum.

Energy is a scalar and Momentum is a 3D vector, these quantities are constants for any closed systems (i.e. with no external forces). So, for example, if we want to calculate the result of a collision between rigid objects, then we can use the conservation of these quantities to give us some information about the state before the collision, if we know the state before. We don't have to interpret what these quantities mean, as far as Newtonian mechanics are concerned they are just numbers being conserved, I don't think we really know what these quantities are. (Perhaps there is some interpretation of these quantities in relativity or quantum mechanics, if you know of one, and its not too difficult to understand, please let me know).

The conservation laws, on their own, are not enough to define how an object behaves. For example, if a wheel is on a hill, it can maintain its energy and momentum whether, or not, it rolls down the hill. But if it can it will roll down the hill, and then when it gets to the valley it rolls up the hill on the other side. To determine whether it rolls down the hill or not, we need to work out the static forces. (Although I wonder if there are any higher order principles about whether a object exchanges one type of energy for another - such as entropy??).

In 3 dimensions the conservation of momentum applies independently in each dimension. Also if there is an external force then its effect can be calculated independently in each dimension.

[Fx,Fy,Fz] = m * [ax, ay, az]

Where force is the sum of all forces on the object. If there is a complex mesh of interlining forces, it may be easier to use numerical methods.

Rotations

Euler developed Newtons laws for the case of rotations, these are similar to the linear laws except:

So for rotation in 2 dimensions, i.e. rotation in a single plane.

Torque = moment of inertia * angular acceleration

In the 3 dimensional case vectors can be used for angular velocities and accelerations (but not for combining 3D angular positions) as explained in kinematics.

However there is a big difference for the rotational case, that is that moment of inertia (I) is different for each axis of rotation, so the equivalent of the f=m*a for the rotation case is given by the following matrix. These Inertia values will be constant if the frame of reference is stationary with respect to the object itself.

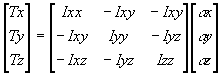
Where:

This means that for a given torque on a system, and if the object is not constrained, then accelerations may be produced in a different direction to the applied torque. This depends on the non-diagonal terms such as Ixy, this means that if an overall torque is produced about the x dimension, and Ixy is non zero then there will be a resulting acceleration about y. This will be greatest when sum(x*y) dm is high, i.e. when there is a lot of mass on the diagonal, in order to think about this, imagine the following extreme example:

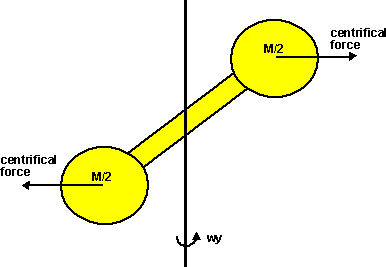
Imagine a rigid object, at 45 degrees to the y axis, with most of its mass at its end points, assuming that its total mass is 2kg (1 kg) at each end, at assume that the position of these masses is [x,y] = [1,1] and [-1,-1].

This would give: Ixx =1, Iyy=1 and Ixy =1.

so:

Tx = ax + ay

Ty = ax + ay

so the result of a torque about y will be an equal acceleration about both the x and y axis.

This means that if the object is unconstrained then it can only rotate about this axis that is shown as diagonal in the above example.

Things can be greatly simplified if the coordinate system can be chosen so that the axis that the object tends to rotate around is aligned with the coordinate system, In the above example above, can be set so that the matrix is diagonal (Ixy == Ixz == Iyz ==0). It is always possible to find at least one frame of reference for an object where this is true.

An different extreme, to the example above,e would be a sphere with evenly distributed mass. In this case the non-diagonal terms for the inertia matrix are always zero, and the sphere will rotate in the direction of the applied torque.

In in-between case might be, for example, a rugby or American football.

Different frames-of-reference

The conservation of energy and momentum apply in any inertial frame of reference provided that we are consistent and apply the rules correctly.

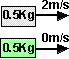
Imagine a 1Kg mass travelling at 1m/s this will have an energy of 0.5J

Now imagine another frame of reference moving at 2m/s, in this frame of reference the 1Kg mass will appear to be travelling at 3m/s this will have an energy of 1J

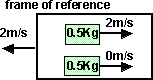
Original frame of reference frame of reference moving at 2 m/s

T = 0.5 m v^2 = 0.5J

In this frame of reference the mass appears to be going at 3 m/s so,

T = 0.5 m v^2 = 0.5*9 = 4.5J

Now split the mass in two, one half is stationary and the other half goes at twice the speed. We do this so that the total mass and momentum remain the same.

Original frame of reference frame of reference moving at 2 m/s

T = 0.5 m v^2 = 0.5*0.5*4J = 1J

In this frame of reference the masses appear to be going at 2 m/s and 4 m/s so,

T = 0.5 m v^2 = 0.5*0.5*16+0.5*0.5*4 = 5J

So changing the frame of reference changes the energy level of the total system but splitting the masses and redistributing the momentum changed the energy by the same amount (0.5J) in each case. So changing the frame of reference changes the 'base' energy level but the energy calculations within that frame of reference are still consistent.

The change in 'base' energy level is 0.5 m v^2

Where

Case 1 - Frame of reference stationary with respect to the object

TX = Ixx ax - Ixy ay - Ixz az
Ty = -Ixy ax +Iyy ay - Iyz az
Tz = - Ixz ax - Iyz ay +Izz az

Case 2 - Frame of reference stationary with respect to the object and body axes aligned with principle axis

If we select the body axes as principle axis then (Ixy == Ixz == Iyz ==0) and the equations can be simplified to:

Tx = Ixx ax
Ty = Iyy ay
Tz = Izz az

Case 3 - Frame of reference moving with respect to the object

In the above case the torques are relative to the frame of reference of the object, this may be appropriate for say, thrusters on a spaceship. However if the torques are applied externally, then we need to work in a frame-of-reference that is not linked to the object. In this case the equations becomes:

Tgx = Ixx ax - Ixy(ay - wx wz) - Ixz(az + wx wy) - (Iyy - Izz)wy wz - Iyz(wy wy - wz wz)
Tgy = Iyy ay - Iyz (az - wx wy) - Ixy (ax + wy wz) - (Izz - Ixx) wx wz - Ixz (wz wz - wx wx)
Tgz = Izz az - Ixz (ax - wy wz) - Iyz (ay + wx wz) - (Ixx - Iyy) wx wy - Ixy (wx wx - wy wy)

(thanks to Mike for correction)

Case 4 - Frame of reference moving with respect to the object and body axes aligned with principle axis

If we select the body axes as principle axis then (Ixy == Ixz == Iyz ==0) and the equations can be simplified to:

Tgx = Ixx ax - (Iyy - Izz) wy wz
Tgy = Iyy ay - (Izz - Ixx) wx wz
Tgz = Izz az - (Ixx - Iyy) wx wy

 

Kinetic Energy

In addition to the conservation rules for linear and angular momentum, there is also another quantity, energy, which must be conserved in any system. Although energy may be converted to other forms such as heat, light, potential energy, etc.

kinetic energy = linear KE + angular KE

linear KE = 1/2 momentum * v = 1/2 m * sqr v

angular KE = 1/2 w H = 1/2 Ixx sqr wx + 1/2 Iyy sqr wy + 1/2 Izz sqr wz - Ixy wx wy - Ixz wx wz - Iyz wy wz

where v = linear velocity of centre of mass

Conservation rules

There are a total of 7 equations which must be true for any given system.

This is not always initiative as in this example.

In the case of a collision of two rigid bodies, each object has 6 degrees of freedom, so there are 12 unknowns to calculate the motions of the bodies after the collision. 12 unknowns and 7 equations, so further information is needed to solve.

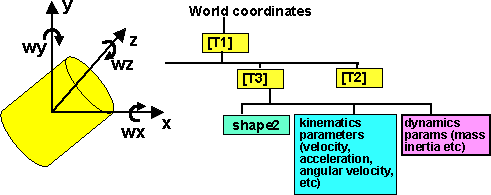
Dynamics information in Scenegraph

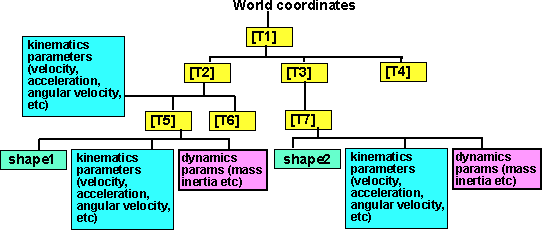
Using a scenegraph structure allows us to define parameters such as inertia in the local frame of reference of the shape.

However when we are calculating the effects of collisions or jointed structure's, we must be sure to do the calculations in the same frame of reference. So we could translate all parameters (inertia, torque, movements) back the world coordinates, or just back to a common point in the tree.

An example - Gyroscopic motion

This is a rotating object aligned with the frame of reference, so we can use the equations from case 4:

Tgx = Ixx ax - (Iyy - Izz) wy wz
Tgy = Iyy ay - (Izz - Ixx) wx wz
Tgz = Izz az - (Ixx - Iyy) wx wy

Since the object is symmetrical about the y axis then Ixx = Izz

also the external torques are zero

This gives:

0 = Ixx ax - (Iyy - Ixx) wy wz
0 = Iyy ay
0 = Ixx az - (Ixx - Iyy) wx wy

rearranging gives:

ax = wz (Iyy - Ixx) wy / Ixx
az = wx (Ixx - Iyy) wy / Ixx

Assuming that wy is high compared to wz and wz it can be considered constant, therefore introduce a constant K=(Iyy - Ixx) wy / Ixx

ax = wz * K
az = -wx * K

So angular acceleration about x produces angular rotation about the z axis and visa-versa.

So provided that wy is high the gyroscope tends to be self stabilising.

Next

This can be used:

I have suggested a dynamics node here

Using multivectors for energy and momentum.

metadata block
see also: go on to dynamics 2

 
Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

 

cover 3d Games: Physics -

 

 

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.

 

cover Dark Basic Professional Edition - It is better to get this professional edition

cover This is a version of basic designed for building games, for example to rotate a cube you might do the following:
make object cube 1,100
for x=1 to 360
rotate object 1,x,x,0
next x

cover Game Programming with Darkbasic - book for above software

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.