Physics - Energy and Momentum of Rotation

Prerequisites

If you are not familiar with this subject you may like to look at the following pages first:

• Energy and momentum
• Solid Bodies

Kinetic Energy of Solid Body

For purely linear motion the kinetic energy of a solid body is:

T = 0.5 m v²

For purely rotational motion the kinetic energy, about its centre of mass, of a solid body is:

T = 0.5 w^t [I] w

So if we have combined linear and rotational motion can we just add the kinetic energy due to these parts separately? I think the answer is no because the energy of a particle is proportional to the square of its velocity. We need to add on another factor:

T = 0.5 m v² + 0.5 w^t [I] w + m(v•(w x r))

This can be derived as follows:

T for particle on solid body = 0.5 sum(mi vi² )

but the velocity of a particle on a solid body is (v + w x r) so the kinetic energy is:

T = 0.5 sum(mi (v + w x r)•(v + w x r))

this can be expanded out to give:

T = 0.5 sum(mi (v² + (w x r)•(w x r) +2v•(w x r))

So, there is a part that is due purely to linear motion, a part that is due purely to rotational motion, and a part that is due to the product of linear motion and rotational motion.

For further information see this page.

Symmetrical body

It might be simplest to start with a symmetrical body, that is for every element of mass on one side of the centre of mass there is an identical element of mass on the other side.

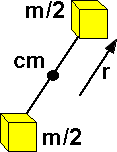
Rotational Energy

The rotational energy is the sum linear energy

rotational energy = linear energy of A + linear energy of B

= 0.5 (m/2) v² + 0.5 (m/2) (-v)²

= 0.5 (m/2) (w r)² + 0.5 (m/2) (-w r)²

= 0.5 m w² r²

= 0.5 I w²

where I = m * r²

In the more general case I is the moment of inertia which in the two dimensional case is the second moment of mass

So

energy of rotation = K = 0.5 I w²

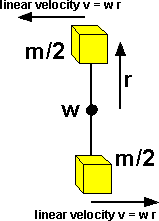
Rotational Momentum

As explained here, the rotational momentum is a different quantity from linier momentum.

L = r x p

where:

• p = m * v
• x = cross product

So, L =m * (r x v)

In two dimensions:

I = m * r²

and v = w r

Which gives, L = I w

So in the example above the inertia for each object is I=m/2 * r² So the total inertia is I=m * r²

So the total angular momentum for the example above is: L=m * r² * w

In this example both w and L are vectors pointing toward the viewer since we are using a right hand coordinate system as explained here.

Next

Combined linier and rotational energy and momentum of solid body

EuclideanSpace

home

Symmetry

Successive Rotations