Introduction
 |
When an object is reflected one of the components of its position is reversed while the other components are not.
The left or right handedness of the object is reversed.
The maths is explained on this page. |
 |
If we now get two mirrors and put them at 90° to each other we can get a view that has been reflected in both mirrors. The object will appear to have been rotated by 180° which is twice the angle between the mirrors.
The left or right handedness of the object is preserved. |
So we can see that 2 reflections in different planes are equivalent to a rotation.
Geometry showing relationship between reflection and rotation
Rotations can be represented as 2 reflections.
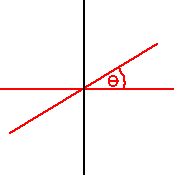
For example if objects are reflected in the two red lines (which are θ degrees apart) then the objects will be rotated by 2 * θ degrees.
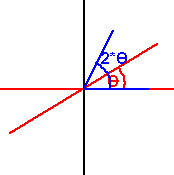
For example, if the blue line along the x-axis is deflected in the x-axis it
does not move, if this is then reflected in the θ line this will result in a line at an angle of 2 * θ.
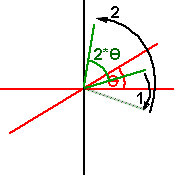
Or, a second example, the green line is first reflected in the x-axis (1),
then reflected in the θ line (2). Again this results in a rotation by an angle of 2 * θ.
Derivation of rotation matrix.
On this page we have derived
the matrix for reflection, so the matrices are:
Reflection in yz
Reflection in θ line
| Px2-Pz* Pz- Py* Py |
2 * Px * Py |
2 * Px * Pz |
| 2 * Py * Px |
Py2-Px*Px- Pz*Pz |
2 * Py * Pz |
| 2 * Pz * Px |
2 * Pz * Py |
Pz2-Py*Py- Px*Px |
where Px,Py and Pz are the endpoints of a unit vector along the θ line.
So to get the rotation by 2 * θ we need to apply these translations one after the other, to represent this we
multiply the matrices:
|
|
* |
| Px2-Pz* Pz- Py* Py |
2 * Px * Py |
2 * Px * Pz |
| 2 * Py * Px |
Py2-Px*Px- Pz*Pz |
2 * Py * Pz |
| 2 * Pz * Px |
2 * Pz * Py |
Pz2-Py*Py- Px*Px |
|
So the following matrix represents the rotation by 2 * θ if Px,Py and Pz are the endpoints of a unit vector along the θ line:
| -Px2 + Pz* Pz + Py* Py |
-2 * Px * Py |
-2 * Px * Pz |
| 2 * Py * Px |
Py2-Px*Px- Pz*Pz |
2 * Py * Pz |
| 2 * Pz * Px |
2 * Pz * Py |
Pz2-Py*Py- Px*Px |
Using Quaternions
We can use quaternions to represent both reflections and rotations, as described here, we therefore have the option to use quaternions to show how to calculate rotation from two reflections.
For Reflection & scaling: P2=q * P1 * q
For Rotation & scaling: P2=q * P1 * q'
- P1 = original position of point in the following format 0 + i x + j y +
k z
- P2 = resulting position of point after transform in the following format
0 + i x + j y + k z
- q = rotation quaternion = qw + i qx + j qy + k qz
- q' = conjugate of q = qw - i qx - j qy - k qz
So we apply the first reflection 'a' to get:
P2=a * P1 * a
then we apply the second reflection 'b' to get:
P2=b * a * P1 * a * b
Expanding out all the terms gives:
out.w= ( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.w +( -b.w*a.x -b.x*a.w -b.y*a.z +b.z*a.y)*in.x +( -b.w*a.y +b.x*a.z -b.y*a.w -b.z*a.x)*in.y +( -b.w*a.z -b.x*a.y +b.y*a.x -b.z*a.w)*in.z
out.x= ( b.w*a.x +b.x*a.w +b.y*a.z -b.z*a.y)*in.w +( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.x +( -b.w*a.z -b.x*a.y +b.y*a.x -b.z*a.w)*in.y +( b.w*a.y -b.x*a.z +b.y*a.w +b.z*a.x)*in.z
out.y= ( b.w*a.y -b.x*a.z +b.y*a.w +b.z*a.x)*in.w +( b.w*a.z +b.x*a.y -b.y*a.x +b.z*a.w)*in.x +( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.y +( -b.w*a.x -b.x*a.w -b.y*a.z +b.z*a.y)*in.z
out.z= ( b.w*a.z +b.x*a.y -b.y*a.x +b.z*a.w)*in.w +( -b.w*a.y +b.x*a.z -b.y*a.w -b.z*a.x)*in.x +( b.w*a.x +b.x*a.w +b.y*a.z -b.z*a.y)*in.y +( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.z
setting in.w=0 gives:
out.w= ( -b.w*a.x -b.x*a.w -b.y*a.z +b.z*a.y)*in.x +( -b.w*a.y +b.x*a.z -b.y*a.w -b.z*a.x)*in.y +( -b.w*a.z -b.x*a.y +b.y*a.x -b.z*a.w)*in.z
out.x= ( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.x +( -b.w*a.z -b.x*a.y +b.y*a.x -b.z*a.w)*in.y +( b.w*a.y -b.x*a.z +b.y*a.w +b.z*a.x)*in.z
out.y= ( b.w*a.z +b.x*a.y -b.y*a.x +b.z*a.w)*in.x +( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.y +( -b.w*a.x -b.x*a.w -b.y*a.z +b.z*a.y)*in.z
out.z= ( -b.w*a.y +b.x*a.z -b.y*a.w -b.z*a.x)*in.x +( b.w*a.x +b.x*a.w +b.y*a.z -b.z*a.y)*in.y +( b.w*a.w -b.x*a.x -b.y*a.y -b.z*a.z)*in.z
if a.w=0 and b.w=0 then we get:
out.w= ( -b.y*a.z +b.z*a.y)*in.x +( b.x*a.z -b.z*a.x)*in.y +( -b.x*a.y +b.y*a.x)*in.z
out.x= ( -b.x*a.x -b.y*a.y -b.z*a.z)*in.x +( -b.x*a.y +b.y*a.x)*in.y +( -b.x*a.z +b.z*a.x)*in.z
out.y= ( b.x*a.y -b.y*a.x)*in.x +( -b.x*a.x -b.y*a.y -b.z*a.z)*in.y +( -b.y*a.z +b.z*a.y)*in.z
out.z= ( b.x*a.z -b.z*a.x)*in.x +( b.y*a.z -b.z*a.y)*in.y +( -b.x*a.x -b.y*a.y -b.z*a.z)*in.z
now if we compare this with an expansion for a rotation we get:
|
= |
| qx*qx+qw*qw-qy*qy- qz*qz |
2*qx*qy- 2*qw*qz |
2*qx*qz+ 2*qw*qy |
| 2*qw*qz + 2*qx*qy |
qw*qw - qx*qx+ qy*qy - qz*qz |
-2*qw*qx+ 2*qy*qz |
| -2*qw*qy+ 2*qx*qz |
2*qw*qx+ 2*qy*qz |
qw*qw - qx*qx- qy*qy+ qz*qz |
|
|
which is nothing like it! what did I do wrong here?
Further Reading
This can be used to generate the matrix representation of the axis angle representation
of rotation:
This site may have errors. Don't use for critical systems.






