Introduction
 |
When an object is reflected one of the components of its position is reversed while the other components are not. The left or right handedness of the object is reversed. |
Reflection of points
We want to reflect point Pa in the plane to give the reflected point Pb.
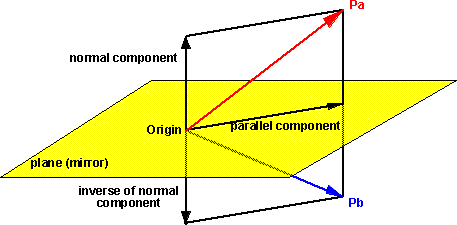
To do this we take a vector from the origin to Pa (the red vector on the diagram above), we then spilt this into its components which are normal and parallel to the plane. We then add these points together again but instead of using the normal we use its inverse.
We can calculate this using Clifford algebra as follows:
Va = (Va*P)/P
That is, multiplying and dividing by P: a vector representing the plane, has no effect. If we now reverse the order of Va and P that will reverse the components parallel to the plane but not the component perpendicular to the plane. However we want to reverse the components perpendicular but not parallel to the plane so we reverse (negative sign) the whole expression to give:
Vb = -(P*Va)/P
where:
- Va = unreflected vector.
- Vb = reflected vector.
- P = Plane represented by normal vector.
- * = Geometric Product.
This is the main result on these pages and it applies when we are working in any number of dimensions (although in a number of dimensions, other than 3, the mirror is not a plane). The result also applies regardless of whether the dimensions square to +ve or -ve, in fact, if the dimensions all square to +ve we can simplify to:
Vb = -(P*Va*P)/(P*P)
= -P*Va*P
The result does require that the dimensions all anti-commute.
This is a very important result as it allows us to calculate rotations in any number of dimensions, on this page, by generating rotations from an even number of reflections.
So all that remains to do here is derive the result using different types of algebras and to look at the implications, especially in higher dimensional spaces.
Perpendicular and Parallel Components
We can calculate this result by more explicitly calculating the perpendicular and parallel components, which were derived On this page so we can combine them as follows,
Va is the sum of its perpendicular and parallel components:
Va = Va || P + Va P
P
and its reflection is:
Vb = Va || P - Va P
P
where:
- Va = vector form origin to Pa
- Vb = vector form origin to Pb
- P = plane, represented by bivector which is normal to plane
from the same page we know that:
- Va || P = (Va
 P) / P
P) / P - Va
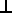 P = Va • P / P
P = Va • P / P
so,
Vb = -(Va • P - Va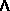 P)/P
P)/P
since • commutes and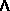 anticommutes reversing the order gives:
anticommutes reversing the order gives:
Vb = -(P • Va + P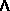 Va)/P
Va)/P
since a • b + a b = a*b we have:
b = a*b we have:
Vb = -(P * Va)/P
Representing Reflection using Different Algebra Types
So to reverse the normal component in different types of algebras we can do the following:
| parallel | perpendicular | parallel + perpendicular (to check if =1) | parallel - perpendicular | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Geometric Algebra | Va • P / P | (Va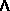 P) / P P) / P |
(Va * P) / P | -(P * Va) / P | ||||||||||||||||
| 2×2 matrix |
|
|
|
|
||||||||||||||||
| tensor | -j*i |
i*j | if i=j then 1 |
if i=j then j*j-i*i else -2ij |
||||||||||||||||
So the final result, expressed in different algebras is:
| Algebra | Transform | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Clifford | p -> - n p n-1 or if all dimensions square to +ve and n is unit length then we can simplify to: p -> - n p n where:
See this page for more details of reflections using Clifford algebra. |
||||||||||||
| Matrix |
assumes orthogonal matrix [M][M]t=1 and det M = -1 otherwise multiply by: 1 / (Px2 + Py2 + Pz2) See this page for more details of reflections using matrix algebra. |
||||||||||||
| Quaternion | Quaternions are considered to be a scalar value and a 3D bivector algebra value. Since, in 3D, vector and bivector algebras are virtually identical we can use quaternions to calculate reflections. Since this only works in 3D and since it can't be combined with other types of transform it is more of a curiosity than a useful technique. See this page for more details of reflections using quaternion algebra. |
Degrees of freedom
Since the vector to Px,Py,Pz is unit length (divided by Px2 + Py2 + Pz2). Therefore reflection has only 2 degrees of freedom, unlike translation and rotation which each have 3 degrees of freedom.
Reflection in more than 3 dimensions
The same equation still applies:
Vb = -(P*Va)/P
and the quantities Vb,Va and P are still vectors but the mirror can no longer be thought of as a plane, the equivalent in 4D for the parallel component would be a directed volume (say a cube).
If P represents the vector which is reversed (perpendicular) this completely specifies the direction of the reflection but we could equally well specify it by the dimensions not reversed which would be the dual of the vector.
| dimensions | dual of vector | meaning |
|---|---|---|
| 2 | vector | both perpendicular and parallel components have one dimension |
| 3 | bivector | reflect in a plane |
| 4 | trivector | reflect in a volume |
Reflection and Translation
Here we have been dealing with pure reflections, that is where the mirror goes through the origin, if we want to offset the mirror then we could:
- Translate our coordinates along the normal so that the origin is moved to intersect the mirror.
- apply Vb = -(P*Va)/P
- Translate our coordinates back by the same distance along the normal in the reverse direction.
Or if we are storing the translation coordinates separately from the direction vectors then we would need to apply the parallel and perpendicular components separately to the translation coordinates.
Further Reading
We can use 2 reflections to represent a rotation, and therefore we can use this analysis to represent rotations by matrices:
