Definition of terms:

• Euler Angles
• Quaternions

This depends on what conventions are used for the Euler Angles. The following assumes NASA Standard Airplane.

The components of the quaternion (w,x,y,z) are:

w = c₁c₂c₃ + s₁s₂s₃
x = c₁c₂s₃ - s₁s₂c₃
y = c₁s₂c₃ + s₁c₂s₃
z = s₁c₂c₃ - c₁s₂s₃

where:

• c₁ = cos(heading / 2)
• c₂ = cos(attitude / 2)
• c₃ = cos(bank / 2)
• s₁ = sin(heading / 2)
• s₂ = sin(attitude / 2)
• s₃ = sin(bank / 2)

An alternative form is:

w = Math.sqrt(1.0 + C₁ * C₂ + C₁*C₃ + S₁ * S₂ * S₃ + C₂*C₃) / 2
x = (C₂ * S₃ + C₁ * S₃ -S₁ * S₂ * C₃) / (4.0 * w)
y = (S₁ * S₃ + C₁ * S₂ * C₃ +S₂) /(4.0 * w)
z = (S₁ * C₂ + S₁ * C₃ - C₁ * S₂ * S₃) / (4.0 * w)

where:

• C₁ = cos(heading)
• C₂ = cos(attitude)
• C₃ = cos(bank)
• S₁ = sin(heading)
• S₂ = sin(attitude)
• S₃ = sin(bank)

Thanks to Mark for letting me know that I originally omitted to point out that the angles are divided by 2 in the first case but not the second. So now the second form is shown upper case (C1) to make it clear that the heading is used directly and not divided by 2. Mark has also included some other useful references.

I don't know which of these forms is most stable? However, as William points out the first is better because it requires the same number of trig operations, no square root, no worry about dividing by zero, uses familiar formulae, and is fairly clearly normalised.

William has proved here that the methods are equivalent.

Derivation

Thanks to Andy for the following:

From the basic definition of a quaternion, we can easily express the quaternion form for rotation along the X, Y, and Z axes, representing bank, attitude, and heading, respectively. Recall that the rotation quaternion (w, x, y, z) for the angle q is encoded as  and (x, y, z) represents a vector of length  along the axis of rotation. Note also that the handedness of the rotation must agree with the handedness of the coordinate system for the quaternion to be valid. Then

To express the rotation of an arbitrary set of Euler angles φ, θ, and ψ we compose the rotations about the three axes by multiplying the quaternions. In the NASA standard aeroplane, the rotations are applied in the order heading, attitude, and bank. However, because each rotation is expressed in the frame of reference of the aircraft, from an outside frame of reference they must be composed in the reverse order. Remember that multiple quaternions are applied right to left:

Substituting and multiplying out, we get

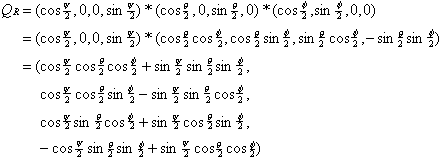
Code

First method (Euler parameter method)

 public final void rotate(double heading, double attitude, double bank) {
    // Assuming the angles are in radians.
    double c1 = Math.cos(heading/2);
    double s1 = Math.sin(heading/2);
    double c2 = Math.cos(attitude/2);
    double s2 = Math.sin(attitude/2);
    double c3 = Math.cos(bank/2);
    double s3 = Math.sin(bank/2);
    double c1c2 = c1*c2;
    double s1s2 = s1*s2;
    w =c1c2*c3 + s1s2*s3;
  	x =c1c2*s3 - s1s2*c3;
	y =c1*s2*c3 + s1*c2*s3;
	z =s1*c2*c3 - c1*s2*s3;
  }

Second method

 public final void rotate(double heading, double attitude, double bank) {
    // Assuming the angles are in radians.
    Double c1 = Math.cos(heading);
    double s1 = Math.sin(heading);
    double c2 = Math.cos(attitude);
    double s2 = Math.sin(attitude);
    double c3 = Math.cos(bank);
    double s3 = Math.sin(bank);
    w = Math.sqrt(1.0 + c1 * c2 + c1*c3 + s1 * s2 * s3 + c2*c3) / 2.0;
    double w4 = (4.0 * w);
    x = (c2 * s3 + c1 * s3 -s1 * s2 * c3) / w4 ;
    y = (s1 * s3 + c1 * s2 * c3 +s2) / w4 ;
    z = (s1 * c2 + s1 * c3 - c1 * s2 * s3) / w4 ;
  }

Example

we take the 90 degree rotation from this:

to this:

As shown here the axis angle for this rotation is:

heading = 0 degrees
bank = 90 degrees
attitude = 0 degrees

so substituteing this in the above formula gives:

• c₁ = cos(heading / 2) = 1
• c₂ = cos(attitude / 2) = 1
• c₃ = cos(bank / 2) = 0.7071
• s₁ = sin(heading / 2) = 0
• s₂ = sin(attitude / 2) = 0
• s₃ = sin(bank / 2) = 0.7071

w = c₁c₂c₃ + s₁s₂s_{3 = 0.7071}
x = c₁c₂s₃ - s₁s₂c_{3 = 0.7071}
y = c₁s₂c₃ + s₁c₂s_{3 = 0}
z = s₁c₂c₃ - c₁s₂s_{3 = 0}

which gives the quaternion _0.7071 + i _0.7071

This agrees with the quaternions here.