Bn - Category of Bundles
A fibre bundle is a function A->I This is described on the following pages: |
 |
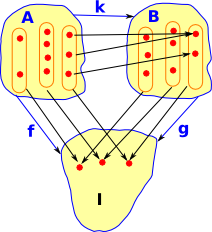
We can make this a category where:
This triangle must commute. So the elements (germs) of a stalk in 'A' must map to the same stalk in 'B'. This is a comma category as discussed on this page. |
 |
We can now look at constructs such as terminal object, pullback and subobject classifier in the Bn Category and see how they correspond to multiple versions of the same constructs in set:
Bn Category - Terminal Object
| The terminal object is a copy of I, this is a bundle of single element sets. |  |
Bn Category - Pullback
 |
More about pullback construct on this page.
Bn Category - Subobject Classifier
Here 'A' has stalks wich are subsets of the stalks in 'B'. The subobject classifier is two copies of 'I' one for 'true' and one for 'false'. |
 |
More about subobject classifier construct on this page.
Section for a Bundle
| Here we reverse the arrow I×2-> I to get I-> I×2. This allows us to pick out the subsets. |  |
Next
The Bn Category can lead on to the concept of a Topos.