Maths - Combine Algebras using Cayley Table

Can we combine Cayley Tables? For instance, imagine we have an algebra defined by table 1 and the elements of this algebra are another algebra defined by table 2. Can we combine these tables to give the overall table which defines the combined algebra?

On this page we look at various posibilities such as:

Direct Product

Perhaps the simplest way to combine (multiply) two sets (and therefore groups) is to use the Cartesian product as explained on this page. This product produces a set from the product:

g×h = {g, h}

So the result of this product is a different type of entity than the elements being multiplied, so the multiplication is not closed, and therefore does not represent a group. The external product makes this into a group because the inputs to the multiplication are also sets:

{g, h} × {g' , h' } = {g * g' , h o h' }

where:

• × is the operation of the combined algebra.
• * is the operation of the group G.
• o is the operation of the group H which may be, or may not be, the same as *.

Variants on Direct Product

Direct Product	{g, h} × {g',h'} = {g * g' , h o h' }
Semidirect Product	{n, h}φ {n',h'} = {n * φ(n') , h o h' }
Bicrossed Product also known as Knit or Zappa-Szep product	{y,z}{y',z' } = {y(z • y'),zy' z'}
Complex Multiplication	(x1,y1)(x2,y2) = (x1x2-y1y2,x1y2+x2y1)

note: the group n is a normal subgroup of the product.

Combining Cayley Tables

The Direct Productworks for commutitive algebras (such as abelian groups) but most of the algebras we are working with have both commutitive and anti-commutitive terms so we can use the Direct Product to determine the type but use other means to determine the sign. So if we want to multiply:

• a e_i
• b e_j

For the type of algebras we are discussing, we could detemine the product of these terms by:

(a e_i)*(b e_j) = a*b*S_ij*(e_ie_j)

where:

• a, b = the scalar values.
• S_ij = represents the sign, it is a step function which is -1 or +1 depending on i and j.
• e_ie_j = represents the type given by the Kronecker product.

S_ij depends on the type of Algebra:

For Clifford algebras it is a Walsh function (or it can be worked out by the number of swaps to order the indicies as described on this page).

For hypercomplex numbers we can use the Cayley-Dickson process.

Direct Sum

One possible way to do this is to use the Direct Sum, So if table1 is:

T1 =a*b	b.1	b.i
a.1	1	i
a.i	i	-1

and table2 is:

T2 =a*b	b.1	b.j
a.1	1	j
a.j	j	-1

then the combined table will be:

T1T2=a*b	b.1	b.i	b.j	b.k
a.1	1	i	0	0
a.i	i	-1	0	0
a.j	0	0	1	j
a.k	0	0	j	-1

Which is fine if we don't want the algebras to interact at all but in most cases this is not what we want so lets go on to other possibilities:

Direct Product

Many algebras are expressed as a linear combination of operators such as:

3 + i 4

or

0.5 + 0.5 e₁₂ + 0.5 e₃₁ + 0.5 e₂₃

Let us generalise a two dimensional quantity as:

a e0 + b e1

where e0 and e1 are operators which are used to distinguish between the two dimensions, a & b are scalar numbers which give the magnitude of each of these dimensions.

We now want to combine this with a second two dimensional quantity:

c e2 + d e3

Can we now combine this into a 4 dimensional algebra with the operators: e0e2, e1e3, e0e3 and e1e2?

An individual term in this algebra would be:

(a e0 + b e1)*(c e2 + d e3)
= ac(e0e2) + bd(e1e3) + ad (e0e3) + bc(e1e2)

e0e0 =

e1e2 =

e0e2 =

e1e0 =

(a,b)(c,d) = (ac - b'd , a'd + cb)

Special Case Double Numbers

Imagine that we have a 2D space defined by 'double numbers' as defined on this page , here we will notate the elements as 'a+e1 b' where e1 is an operator denoting the dimension. So the multiplication rule will be given by:

(a+e1 b)*(c+e1 d) = (ac + bd) + e1 (ad + bc)

In other words we just multiply out the terms as we would normally and where the dimension of the resulting term is given by this table:

T1 = X*Y	y.1	y.e1
x.1	1	e1
x.e1	e1	1

Now suppose we want to combine the above 2D space with a completely separate 2D space to give a 4D space. The multiplication rule for the second space is also formed from double numbers as defined by this table:

T2 = X*Y	y.1	y.e2
x.1	1	e2
x.e2	e2	1

The table for the combined 4D table can be generated by making the elements of space 1 to be not real numbers but elements of space 2.

Attempt to use Kroecker Product

Lets try generating the combined table using the kroecker product [T1][T2]:

[T1][T2]=

1 e1 e1 1 1 1 e1 e2 1 e2 1 e1 e1 1 e2 1 e1 e1 1 1

multiplying out we get:

[T1][T2]=

1 e1 e2 e1e2 e1 1 e1e2 e2 e2 e1e2 1 e1 e1e2 e2 e1 1

We can continue the process indefinitely, each new double that we use multiplies the dimension by 2, so another term gives:

[T1][T2][T3]=

1 e1 e2 e1e2 e1 1 e1e2 e2 e2 e1e2 1 e1 e1e2 e2 e1 1 1 1 e1 e2 e1e2 e1 1 e1e2 e2 e2 e1e2 1 e1 e1e2 e2 e1 1 e3 1 e1 e2 e1e2 e1 1 e1e2 e2 e2 e1e2 1 e1 e1e2 e2 e1 1 e3 1 e1 e2 e1e2 e1 1 e1e2 e2 e2 e1e2 1 e1 e1e2 e2 e1 1 1

Again multiplying out we get:

[T1][T2][T3]=

1 e1 e2 e1e2 e3 e1e3 e2e3 e1e2e3 e1 1 e1e2 e2 e1e3 e3 e1e2e3 e2e3 e2 e1e2 1 e1 e2e3 e1e2e3 e3 e1e3 e1e2 e2 e1 1 e1e2e3 e2e3 e1e3 e3 e3 e1e3 e2e3 e1e2e3 1 e1 e2 e1e2 e1e3 e3 e1e2e3 e2e3 e1 1 e1e2 e2 e2e3 e1e2e3 e3 e1e3 e2 e1e2 1 e1 e1e2e3 e2e3 e1e3 e3 e1e2 e2 e1 1

If we are using Clifford algebra then we leave multiplied dimensions like e1e2 as they are be bivector bases as opposed to single terms like e1 which are vector bases. Similarly e1e2e3 is left as a trivector.

For the type of algebras we are generating here, lets call them hypercomplex algebras, then we replace terms like e1e2 with a normal vector term say e3 at each iteration before multiplying in the next term.

This is almost correct, it gives the dimension for many of the algebras that we commonly use: complex numbers, quaternions, octonions, Clifford algebras, etc. have this structure.

The difference in all cases is the sign of the term.

Calculating these tables using a Computer program

From the indexes of the terms that we want to multiply together we can easily calculate the required product term from the bitwise exclusive or of the two indices.

For example, say we want to multiply index 6 by index 4, the binary values of these indexes are 110 and 100 so the bitwise exclusive or is:

110
100
---
010

giving the result 2. This works as long as the indexes are in bit order.

The reason this works is that, if any dimension occurs in both multiplicands, then it cancels out and does not appear in the result.

As stated before, finding the type of dimension in this way is easy, the problem is finding the sign.

Can we Modify the Kroecker Product to correct the sign?

C

[T1]×[T2]=

1 e1 e1 1 1 1 e1 e2 1 e2 e2 1 e1 e1 1 1 1 e1 e1 1

multiplying out e2e1= -e1e2 we get:

[T1]×[T2]=

1 e1 e2 e1e2 e1 1 e1e2 e2 e2 -e1e2 1 e1 -e1e2 e2 e1 1

Generating algebras from algebras

As we have said we cant use this method for other types because the sign changes.

To take the simplest possible example, When we have complex numbers whose elements are complex numbers, can we use the complex number table to derive the table for quaternions?

So can we take the table1 for complex numbers:

a*b	b.1	b.i
a.1	1	i
a.i	i	-1

and table2 for complex numbers:

a*b	b.1	b.j
a.1	1	j
a.j	j	-1

and derive the table for quaternions:

a*b	b.1	b.i	b.j	b.k
a.1	1	i	j	k
a.i	i	-1	k	-j
a.j	j	-k	-1	i
a.k	k	j	-i	-1

From this we can see that table 1 & 2 are subsets of the required tables but there are still some squares not filled in. To do this we need some further information about the way that i and j combine, for instance:

• k = ij
• k = -ji (i and j anticommute)
• kk = -ijji = -1

Is there some systematic way that we can determine the minimum extra information to complete the overall table?

If i and j commute: k = ij = ji then we can combine the two tables by taking the kronecker product:

a*b	b.1	b.i	b.j	b.k
a.1	1	i	j	j*i
a.i	i	-1	j*i	j*(-1)
a.j	j	j*i	(-1)	(-1)*i
a.k	j*i	j*(-1)	(-1)*i	(-1)*(-1)

which gives the following table, the highlighted values are inverted if i and j anti-commute (as for quaternions):

a*b	b.1	b.i	b.j	b.k
a.1	1	i	j	k
a.i	i	-1	k	-j
a.j	j	k	-1	-i
a.k	k	-j	-i	1

How can we scale this up to larger tables?

Lets make it a bit more general and represent the first tables as:

a*b	a	b
a	aa	ab
b	ba	bb

and:

a*c	a	c
a	aa	ac
c	ca	cc

So we have the values highlighted below:

	a	b	c	d
a	aa	ab	ac	ad
b	ba	bb	bc	bd
c	ca	cb	cc	cd
d	da	db	dc	dd

kronecker product

It would be nice if we could combine the two tables more mechanically, I tried :

a*b	b.1	b.i
a.1	1	i
a.i	i	-1

and table2 for complex numbers:

a*b	b.1	b.j
a.1	1	j
a.j	j	-1

This gives the following kronecker product:

a*b	b.1	b.i	b.j	b.k
a.1	1*1	1*i	j*1	j*i
a.i	1*i	1*(-1)	j*i	j*(-1)
a.j	j*1	j*i	(-1)*1	(-1)*i
a.k	j*i	j*(-1)	(-1)*i	(-1)*(-1)

Multiplying out the terms gives the following, this gives the right du" :

a*b	b.1	b.i	b.j	b.k
a.1	1	i	j	k
a.i	i	-1	k	-j
a.j	j	k	-1	-i
a.k	k	-j	-i	1

 

first tables as:

a*b	a	b
a	aa	ab
b	ba	bb

and:

a*c	c	d
c	cc	cd
d	dc	dd

So we have the values highlighted below:

	a	b	c	d
a	aa cc	aa cd	ab cc	ab cd
b	aa dc	aa dd	ab dc	ab dd
c	ba cc	ba cd	bb cc	bb cd
d	ba dc	ba dd	bb dc	bb dd

Generating valid Algebras

I don't know if there is a systematic way to generate all possible algebras? Here are a couple of possibilities:

 

doubling up

This is more applicable to widely used algebras such as complex numbers and quaternions. We start with a simple 2D table:

e0	e1
e1	e0

In each of these elements we put a copy of another table:

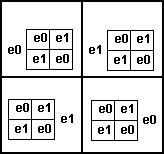
Where the outside element is e1 we add dimension (2) to the corresponding elements as follows:

e0	e1	e2	e3
e1	e0	e3	e2
e2	e3	e0	e1
e3	e2	e1	e0

We can continue to double up as follows, for the next stage we add dimension (4) as follows:

e0	e1	e2	e3	e4	e5	e6	e7
e1	e0	e3	e2	e5	e4	e7	e6
e2	e3	e0	e1	e6	e7	e4	e5
e3	e2	e1	e0	e7	e6	e5	e4
e4	e5	e6	e7	e0	e1	e2	e3
e5	e4	e7	e6	e1	e0	e3	e2
e6	e7	e4	e5	e2	e3	e0	e1
e7	e6	e5	e4	e3	e2	e1	e0

Signs

Complex numbers and quaternions have signs:

e0	e1
e1	-e0

As before, I tried to combine the tables:

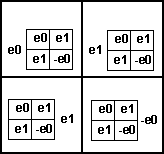
The signs don't seem to work in this way, we are trying to get to this:

e0	e1	e2	e3
e1	-e0	e3	-e2
e2	-e3	-e0	e1
e3	e2	-e1	-e0

The terms not on the unity row & column or leading diagonal are asymmetrical

+	+	+	+
+	-	+	-
+	-	-	+
+	+	-	-

The only way I can see to do this is to flip the table (top to bottom) in the bottom row:

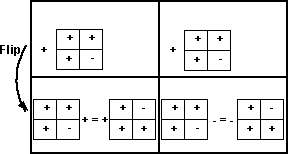
However this does not seem to work when we double up to 8D:

0	1	2	3	4	5	6	7
1	-0	3	-2	5	-4	-7	6
2	-3	-0	1	6	7	-4	-5
3	2	-1	-0	7	-6	5	-4
4	-5	-6	-7	-0	1	2	3
5	4	-7	6	-1	-0	-3	2
6	7	4	-5	-2	3	-0	-1
7	-6	5	4	-3	-2	1	-0

To make the negatives stand out I have highlighted them here:

+	+	+	+	+	+	+	+
+	-	+	-	+	-	-	+
+	-	-	+	+	+	-	-
+	+	-	-	+	-	+	-
+	-	-	-	-	+	+	+
+	+	-	+	-	-	-	+
+	+	+	-	-	+	-	-
+	-	+	+	-	-	+	-

But I can't get to it from here:

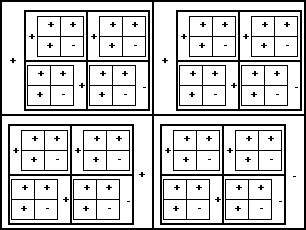
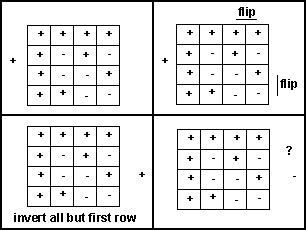
Perhaps there is not a short cut and the sign of each element has to be worked out from first principles?

 

EuclideanSpace

home

Prerequisites

• Cartesian product for sets.
• Combining Groups

Generating Geometric Algebras

Group Theory