Representation theory is related to group theory except that we look at this in terms of linear algebra such as matrices. In other words we are looking at the symmetries of vector spaces. A simple example is Pauli matrices.
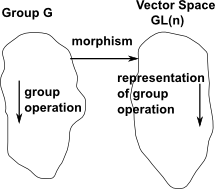
Construction of Representations
- From Permutation Groups
- By combining two other Representations
- From Invariant Subspaces
From Permutation Groups
Cyclic Group
We can construct a matrix that has the property that [M]n = [1] in several ways including:
- Calculate n√[1] by using the methods on this page.
- If the permutation maps (1,2,3) to (2,3,1) then we create a matrix with all zeroes except the first column has 1 in the 2nd row, the next column has 1 in the 3rd row, the last column has 1 in the 1st row. So the (2,3,1) represent the sequence of rows where we set 1s.
The second method produces a very large matrix because the matrix contains only 0's and 1's.
Example of a Cyclic Group Representation using a Program
We can use a computer program to show that this works, here I have used Axiom/FriCAS which is described here.
m:= matrix [[0,0,1],[1,0,0],[0,1,0]]
Type: Matrix(Integer)
m*m
Type: Matrix(Integer)
m*m*m
Type: Matrix(Integer)
(4) ->
|
Combining Cycles
We can create a representation of any permutation (and therefore of any group) by generating the representation for each cycle separately. That is each one is a seperate generator.
By combining two other Representations
If U and V are representations of a group then
- The direct sum U
 V
V - The direct (Kronecker) product U
 V
V
Are also representations.
The identity for vector space is also true for representations:
V![]() (U
(U W) = (V
W) = (V![]() U)
U) (V
(V![]() W)
W)
From Invariant Subspaces
There is a common theme to:
- Invariant subspace
- Eigenvectors
- Idempotent element
Which is related to the idea of symmetry, somthing which does not change during a transform.
(1) -> t:= matrix [[1,2],[0,4]]
+1 2+
(1) | |
+0 4+
Type: Matrix(Integer)
(2) -> t*t
+1 10+
(2) | |
+0 16+
Type: Matrix(Integer)
(3) -> t*t*t
+1 42+
(3) | |
+0 64+
Type: Matrix(Integer)
(4) ->
|
From Clifford Algebra
Generating Representations from other Representations
If we already know a representation of a given group then how can we find other 'equivalent' representations?
| group | group representation | other representation | |||||||||||
| g | --> | [G] | --> | f([G]) | |||||||||
| h | --> | [H] | --> | f([H]) | |||||||||
|
|
|
|||||||||||
| g•h | --> | [G•H])= [G]*[H] | --> | f([G•H])= f([G]*f([H]) |
If we can find some matrix function f() the preseves the multipication so that:
f([G•H])= f([G]*f([H])
Then we can use that to generate a new representation, an example is the determinant,
det([G•H])= det([G]*det([H])
Of course this representation contains a lot less information and so can't reconstruct the original group.
The action of a linear transform has a quadratic form:
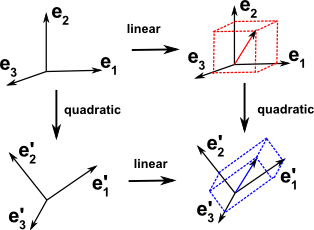
More about the quadratic form of rotations on this page.
Two representations are equivalent if they are related by a 'similarity' transformation.
If D(G) is a representation of a group G.
and D'(G) is an equivalent representation of a group G.
then:
D'(g) = T-1•D(g) • T
where:
- T = transformation
- g = element of G

