Inverse
Here we look at the multiplicative inverse of multivector 'm', that is '1/m'. On this page we saw that the inverse of a pure vector is the same vector with a scaling factor.
On the same page we saw that the inverse of a bivector blade is calculated by replacing the bivector bases with their reverse (with a scaling factor). Taking the reverse of a bivector is the same as chaging its sign. There is a problem in 4D and above though, the non-scalar terms may not cancel outcancel out because bivectors like e12 and e34 don't have a common term. So do four dimensional bivectors allways have a multiplicative inverse?
So how can we calculate the inverse for a general bivector based in 4D which contains upto 6 terms? The inverse of any two terms with a common term is the reverse, but if there is no common term the result is more complicated as we have seen.
General Bivector Case
We want to find the most general case for the inverse of a 4D bivector.
1/ (a e12 + b e31 + c e23 + d e41 + f e42 + g e43)
we start by multiplying the top and bottom by the conjugate:
(-a e12 - b e31 - c e23 - d e41 - f e42 - g e43)
multiplying all the terms out gives the following denominator:
a² + b² + c² + d² + f² + g² + 2*(a*g + b*f + c*d)e1234
this is quite long so lets substitute:
x = a² + b² + c² + d² + f² + g²
y =2*(a*g + b*f + c*d)
so the denominator is:
x + y e1234
to get rid of the e1234 term we will multiply top & bottom by,
x - y e1234
so the inverse is:
(-a e12 - b e31 - c e23 - d e41 - f e42 - g e43)(x - y e1234)/(x² - y²)
= ((g y -a x) e12
+ (f y - b x) e31
+ (d y - c x) e23
+ (c y - d x) e41
+ (b y - f x) e42
+ (a y - g x) e43)/(x² - y²)
where:
- x = a² + b² + c² + d² + f² + g²
- y =2*(a*g + b*f + c*d)
Inverse of 4D Trivector
1/(a e123 + b e142 + c e134 + d e324)
is equal to
(-a e123 - b e142 - c e134 - d e324)/(a² + b² + c² + d²)
So we don't have the same problem for trivectors that we had for bivectors, in 4d we can just use the reverse of all the terms, with the appropriate scaling factor.
Inverse of 4D Quadvector
1/(a e1234) = (1/a) e1234
There is only one quadvector in 4D which is its own inverse.
Example
Lets try inverting the bivector: a e12 + b e34, this multiplying top & bottom by the reverse gives:
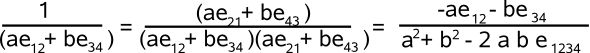
So the denominator still has a non-scalar term, we can make another attempt to canel it out by multipling by its reverse, so the numirator is,
(a e21 + b e43)(a² + b² + 2ab e1234)
= (a (a² + b²) - 2ab²) e21 + (b (a² + b²) - 2a²b) e43
= (a (a² - b²)) e21 + (b (b² - a²)) e43
= (a (a + b)(a - b)) e21 + (b (b - a)(b + a)) e43
and the denominator is:
(a² + b² - 2ab e1234)(a² + b² + 2ab e1234)
= (a + b)²(a² + b² - 2 a b)
so the result is:
= (a (a - b)/((a + b)(a² + b² - 2 a b))) e21
+ (b (b - a)/((a + b)(a² + b² - 2 a b))) e43
This looks very messy. Can it be simplified and further?
