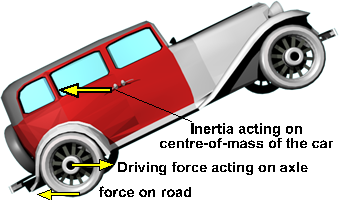
Movement in a line
On this page we are looking at the situation where the steering wheels are pointing straight ahead. In the next page we will go on to cornering.
Orientation
Since the car is driving in a straight line, we only need to model its movement in 2 dimensions. In two dimensions there is only one direction of rotation, the orientation of the car can therefore be represented by the angle: theta. (we will model any rocking of the car on its springs separately so it is ignored here).
However, we want to update the position of the car in every frame, to derive this from the angle theta would require the calculation of sin(theta) and cos(theta) in every frame. It is therefore more efficient to store the orientation of the car by a two dimensional vector [dir]. This is a unit length vector which points in the direction of the car, so,
[dir] = [sin(theta), cos(theta)]
This can be represented as a normalised complex number as explained on this page. This will allow rotations to be combined by multiplying complex numbers.
Position
First lets assume that the velocity is constant. Since we are traveling in a straight line we can use the 1 dimensional (scalar) equations of motion and multiply them by the direction vector to give the position in 2 dimensions:
[s] = (s(0)+v(0)*t)[dir]
where:
- [s] = position of centre of mass as a function of time, this is a 2D vector value.
- s(0) = position along the vector at time=0, this is a scalar value.
- v = constant velocity, this is a scalar value.
- t = time, this is a scalar value.
- [dir] = unit direction vector, this is a 2D vector value.
The time t, is the time since the start of the simulation, if the frames of the animation are generated at a constant rate then, we can just increment t by a fixed amount each frame. This will add a fixed 2D vector value to the position each time.
Now lets look at the situation where the car is accelerating or decelerating, it will then follow this equation:
[s] = (s(0)+v(0)*t+ 0.5 a*t2)[dir]
where:
- a = constant acceleration, this is a scalar value.
- v(0) = velocity at time t=0, this is a scalar value.
- other values as above.
So how do we represent the status of the car, in the program, so far? That is, the values that might possibly change in every frame, I think we need to hold the following structure:
public class carStatus {
vector2d s // position of the centre of mass, integral of v,
vector2d v // velocity, integral of a,
vector2d a // acceleration, depends only on forces acting at the time.
}
In this case these values are scalars, however the next page covers turning, so we will eventually have to store each of these as vectors.
Forces & Torques - Starting & Stopping
As explained already, we are modeling the movement of the car separately from the suspension of the car, the suspension part is explained on this page. We need to relate this to the motion of the car, discussed on this page, the forces are related to the acceleration.
The engine generates a torque on the wheel (a torque is a set of forces which tends to cause rotation). This causes a linear force on the axle which tends to move the car forward. The acceleration of the car produces an equal and opposite force (F = m*a) acting on the centre of mass of the car.
Since the inertia force is laterally displaced from the driving force, this tends to produce another torque, which tries to rotate the whole car. This will tend to increase the downforce on the back wheel and decrease the downforce on the front wheel. In an extreme case this could rotate the whole car.
On this page we have explored movement in a straight line, on the next page we extend this to cornering.
|
metadata block
|
|
|
| see also: |
|
| Correspondence about this page |
|
|
Book Shop - Further reading.
Where I can, I have put links to Amazon for books that are relevant to
the subject, click on the appropriate country flag to get more details
of the book or to buy it from them.
|
Game Programming for Teens.
other games programming books
|
|
Commercial Software Shop
Where I can, I have put links to Amazon for commercial software, not
directly related to this site, but related to the subject being discussed,
click on the appropriate country flag to get more details of the software
or to buy it from them.
|
other commercial software
|
|
Can this page be improved?
Please send me any improvements to
here. I would appreciate ideas to make the pages more useful including
error correction, ideas for new pages, improvements to wording. It helps
if you quote the full URL of the page.
|
|
|
progam
I am working on a project which uses these principles, if you would like
to help me with this you are welcome to join in, here:
|
http://sourceforge.net/projects/mjbworld/
|
This site may have errors. Don't use for critical systems.
