Line intersection
The intersection of two lines, if they do intersect, is a point.
If we have lines of infinite length then they will intersect unless the lines are parallel.
What is the best way to specify a line? In this case we want to work with finite length so a good way to specify the line is by its end points. In order to find the intersection of lines we need to convert this to the equation of the line: y = a*x + b as follows:
If the endpoints are: P1 and P2, then,
P1.y = a * P1.x + b
P2.y = a * P2.x + b
substituting for b gives:
P1.y - a * P1.x = P2.y - a * P2.x
a * (P2.x - P1.x) = (P2.y - P1.y)
therefore:
a = (P2.y - P1.y)/(P2.x - P1.x)
b = (P2.x*P1.y - P1.x*P2.y)/(P2.x - P1.x)
similarly, if we have a second line from P3 to P4 given by the equation y = c*x + d,
then we can find the intersection by solving the simultaneous equations:
y = a*x + b
y = c*x + d
substituting for y gives:
a*x + b = c*x + d
x * (a - c) = (d - b)
therefore the point of overlap is:
x = (d - b)/(a - c)
y = (a*d- b*c) /(a - c)
where:
- a = (P2.y - P1.y)/(P2.x - P1.x)
- b = (P2.x*P1.y - P1.x*P2.y)/(P2.x - P1.x)
- c = (P4.y - P3.y)/(P4.x - P3.x)
- d = (P4.x*P3.y - P3.x*P4.y)/(P4.x - P3.x)
These lines overlap if this point is between P1 and P2 and also between P3 and P4.
Bounding Circles
The shape of overlapping circles is quite complicated and I'm not sure there is an easier way to specify the shape of intersecting circles than by specifying the two circles.
This is the easiest way to detect collisions because a circle is independent of alignment.
Two circles overlap if the sum of there radii is greater than the distance between their centers. Therefore by Pythagoras we have a collision if:
(cx1-cx2)2 + (cy1-cy2)2 < (r1+r2)2
where:
- cx1,cy1 = centre x and y coordinates of circle 1
- cx2,cy2 = centre x and y coordinates of circle 2
- r1 = radius of circle 1
- r2 = radius of circle 2

Triangles
The intersection of two triangles could be a 3 to 6 sided polygon.
In order to check if the triangles do overlap we need to look round the triangles to see if there is clear space between the two triangles. In order to do that, in a way that can be done by a computer, we project all the points on both triangles onto a line. If we can find a line which has the points of one triangle and one end and the points of the other triangle at the other end then we have found a gap between the two triangles and they don't overlap.
How do we find a line orientation that will find the gap (if it exists) between the two triangles? Well we could try all possible orientations from 0 to 360 degrees but we don't have to do this. If we try the 6 orientations perpendicular to the sides of both triangles that should do it.
Triangle and Line
Bounding Rectangles
axis aligned
How do we detect when these rectangles overlap? If the axis of the rectangles are aligned it is easy to check if they overlapped
non-axis aligned
.
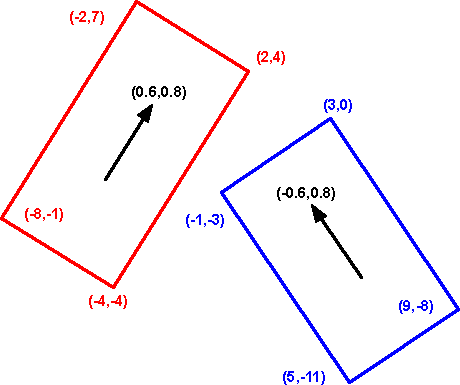
If we were checking for a collision in the physical world we could walk around the objects, if we could see could see a gap between the objects from any direction, then the objects cant be overlapping.