Sources of Documentation
Install Coq
Instructions available here:
https://github.com/coq/coq/wiki/Installation-of-Coq-on-Linux
| Coq is not available directly on openSUSE so I installed from open build service. |  |
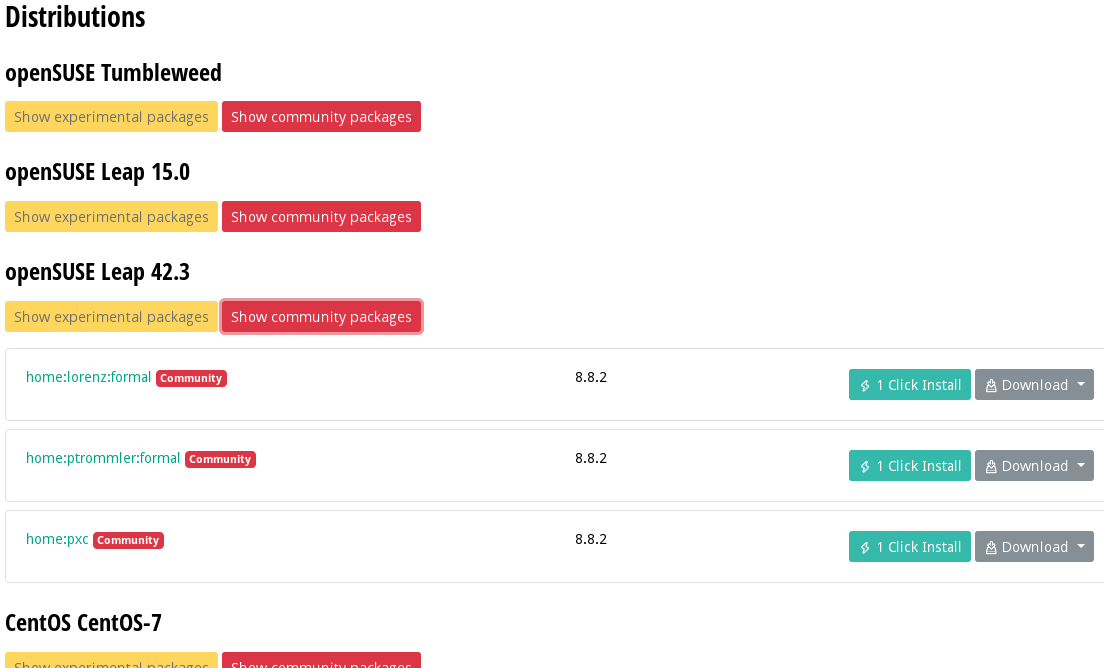 |
installs in:
- //usr/lib64/coq
- //usr/lib64/ocaml
Install Proof-General
Assuming Emacs with melpa is already installed (if not see this page ) install proof-general into Emacs:
Install proof-generalM-x package-refresh-contents M-x package-install <cr> |
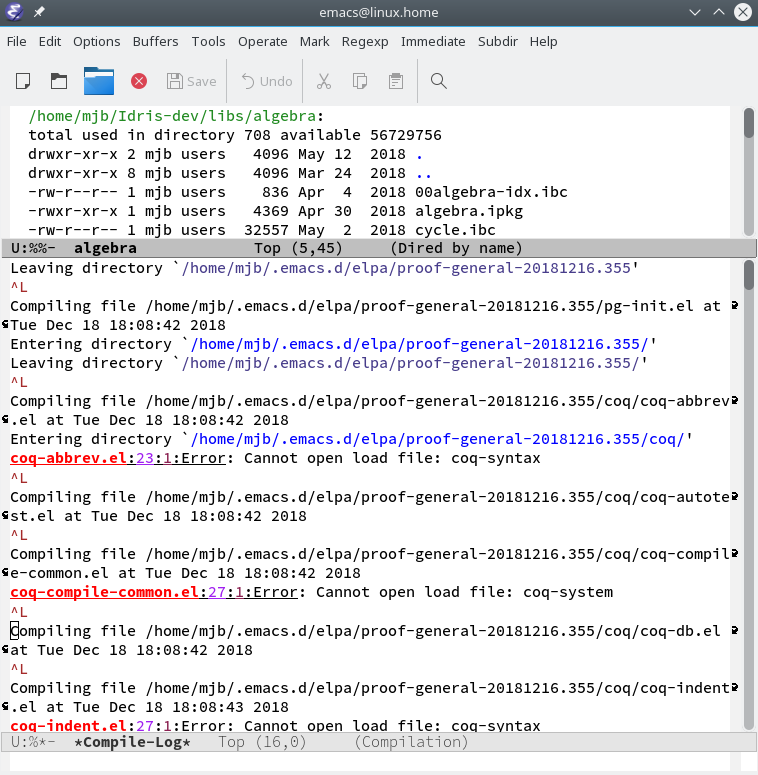 |
Using Coq
Gallina is the specification language of Coq:
https://coq.inria.fr/refman/language/gallina-specification-language.html
It is important that this language cannot prove false. Because of this the language is not turing complete, it always terminates (has weak normalization property).
Types in Gallina
:Type - hierarchy of types
:Prop - propositions are outside this hierarchy
Gallina is a programming language with dependant and inductive types. Every function is total.
Examples
| data: | Inductive day : Type := | monday : day | tuesday : day | wednesday : day | thursday : day | friday : day | saturday : day | sunday : day. |
| functions: | Definition next_weekday (d:day) : day := match d with | monday => tuesday | tuesday => wednesday | wednesday => thursday | thursday => friday | friday => monday | saturday => monday | sunday => monday end. |
Examples
Function (lambda) examples.
The tools such as proof-general allow proofs to be derived interactivly. Each tactic used changes some internal proof state. So we are, sort of, seralising the proof. |
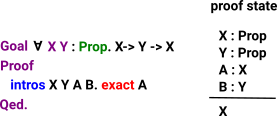 |
| Instead of specifying A & B we could specify lambda. | 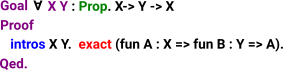 |
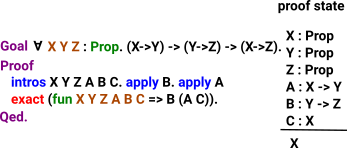 |
introsTakes hypothisis and puts into context, Use when we have implication or forall. Constucts a lambda |
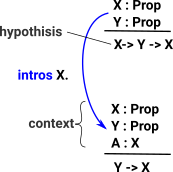 |
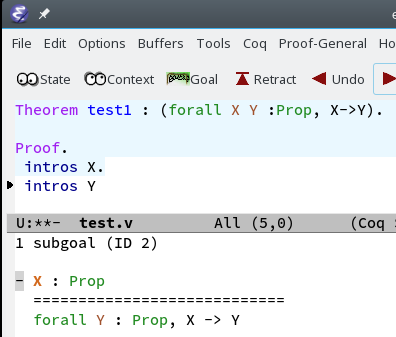
| At the start of the proof the context is empty and the assumptions are part of the conclusion. | 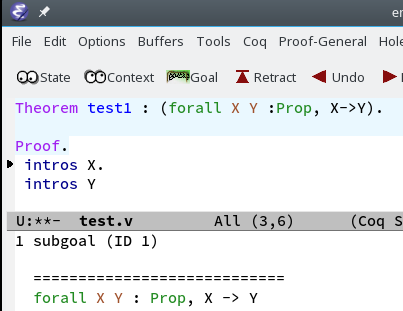 |
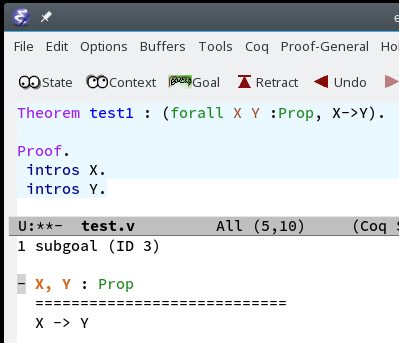
When we step to intros X this moves X:Prop to the context. |
 |
 |
|
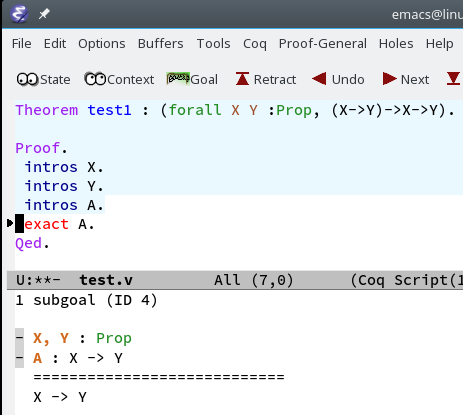 |
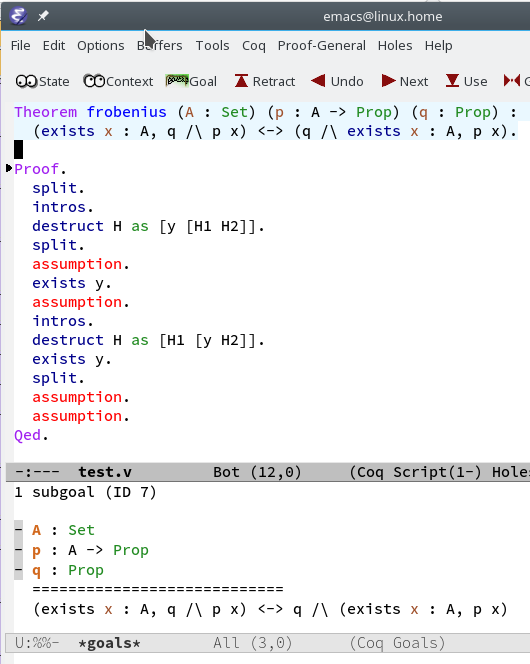
Proofs with Quantifiers
 |
|
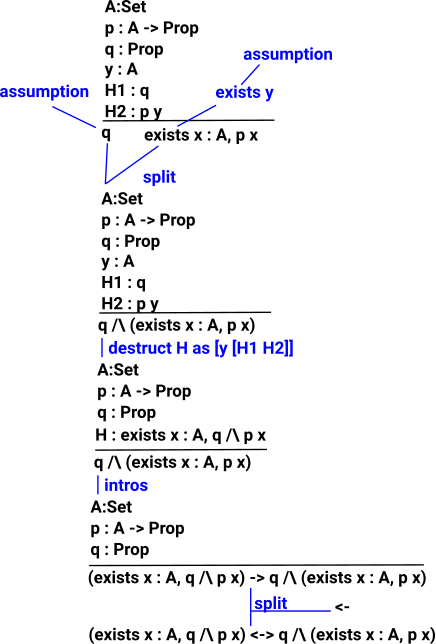 |
Tactics
Syntax
| Check | |
| let | |
| Eval x in | |
| Inductive x := | Define a type (data) x by giving its constructor. |
| Definition x := | Define a constant, could be a function |
| Require Import | Load a library, for instance:
|
| Open Scope | |
| Locate | |
| Fixpoint | Define a recursive function. |
| Notation "( x , y )" := (pair x y). | Allows us to define an alternative notation. |
Example, |
These keywords mean the same thing. |
Proof
<tactic>
<tactic>...
QED. |
Tactics tell Coq how it should check the correctness of some claim we are making |
Proof
<tactic>
<tactic>... |
give up trying to prove this theorem and just accept it as a given. |
Tactics:
| reflexivity. | both sides of equation are the same |
| simpl. | simplify |
| intros H. | Move the hypothesis H into the context. Allows us to reason by assuming the hypothesis |
| rewrite -> H. | Rewrite the goal using the hypothesis H |
| destruct n as [| n']. | n is variable name to be introduced |
| apply | apply a function. So if we have (X->Y) and X we can apply to get Y. |
| unfold | |
| assert | Allows large proofs to be broken into sub-proofs, we can assert and prove in place, rather than creating external top level proofs. |
Comparing Coq to Idris
In order to get some insight into the design of Coq I think it helps to compare it with other programs. So here is a comparison with Idris (see this page), Idris is a more general language but it also does proofs.
| Coq | Idris | |
|---|---|---|
| Booleans | Inductive bool : Type := | true : bool | false : bool. |
data Bool = False | True |
| not | Definition negb (b:bool) : bool := match b with | true => false | false => true end. |
not : Bool -> Bool not True = False not False = True |
| and | Definition andb (b1:bool) (b2:bool) : bool := match b1 with | true => b2 | false => false end. |
(&&) : Bool -> Lazy Bool -> Bool (&&) True x = x (&&) False _ = False |
| or | Definition orb (b1:bool) (b2:bool) : bool := match b1 with | true => true | false => b2 end. |
(||) : Bool -> Lazy Bool -> Bool (||) False x = x (||) True _ = True |
| Numbers | Inductive nat : Set := | O : nat | S : nat -> nat. |
data Nat : Type where
Z : Nat
S : Nat -> Nat
|
| plus | Fixpoint plus (n m : nat) : nat :=
match n with
| O => m
| S n' => S (plus n' m)
end. |
plus : Nat -> Nat -> Nat plus Z m = m plus (S k) m = S (plus k m) |
Theorem plus_O_n : forall n:nat, 0 + n = n. Proof. simpl. reflexivity. Qed. |
plusReduces : (n:Nat) -> plus Z n = n plusReduces n = Refl |
|
x |
plusReducesZ : (n:Nat) -> n = plus n Z plusReducesZ Z = Refl plusReducesZ (S k) = cong (plusReducesZ k) |
|
x |
x |
|
x |
x |
|
x |
x |
|
x |
x |
|
x |
x |
|
x |
x |
|
x |
x |
|
HoTT
Idris and HoTT:


