On this page we will look at the curvature of lines, surfaces and higher order objects. In order to see this curvature we will embed these objects in a space with one extra dimension. For instance:
- A line has 1 dimension so we will view it in 2 dimensions.
- A surface has 2 dimensions so we will attempt to depict it as a 3 dimensional view.
Curvature is a scalar field, that is there will be a scalar value corresponding to every point on the object.
Curvature of a Line
If the curvature (K) is the same at every point on the line then the line forms a circle. The radius of this circle will be r = 1/K.
So how can we calculate the curvature at every point on any line? One first guess might be the second differential (the rate of change of the slope of the line) but this does not work as we shall see:
|
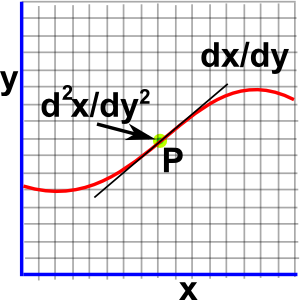 |
This formula would give a negative curvature on one side of a circle and a positive curvature on the other side of the circle which is obviously wrong. We need to amend the formula as follows to make it work.
| curvature = | ∂² x | ||
| ___∂ y²___ | |||
| [ 1 + ( | ∂ x | )² ]3/2 | |
| ∂ y | |||
| At this point the second differential is positive, that is: as we travel along the line the slope increases. |  |
| At this point the second differential is negative, that is: as we travel along the line the slope decreases. |  |
| At this point the curvature is zero, that is: as we travel along the line the slope is at an inflection point between increasing and decreasing. | 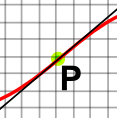 |
Curvature of a Surface
Despite the fact that the surface is two dimensional, the curvature is a scalar (I should say real) value at every point, not a vector.
In the same way that: for a line, a constant (non zero) curvature will produce a circle so, for a surface, a constant (positive) curvature will produce the surface of a sphere.
However, unlike a line, a surface (at each given point) can have either positive or negative curvature.
| To start with the simple case of a flat plane then the curvature at every point is zero. (equicalent to an infinite diameter sphere) |  |
| If we now take part of the surface of a sphere, which meets the plane, with the curvature in both dimensions turning toward us, we will have a positive curvature. |  |
| If we now take a similar subsection of a sphere, but on the other side of the plane, with the curvature in both dimensions turning away from us, we will have a positive curvature. |  |
| If we now take a surface with the curvature in one dimension turning toward us and the other dimension turning away from us, so we have a saddle, we will have a negative curvature. |  |
Non Euclidean Geometry
So far we have visulalised these curved spaces by looking at them from a higher dimensional space. However it is possible to investigate them within their own dimensions by using a definition of distance (known as the metric) which gives the required curvature.
When we investigate the geometry of curved space we find that it is very similar to Euclidean geometry except that they don't have the property that there is only one line, parallel to a given line, that goes through a given point.
- Constant positive curvature space does not have any parallel (non-intersecting) lines.
- Constant negative curvature space has many parallel lines.
This leads to many variations on the geometry, for example Pythagoras:
- Euclidean Space: hypotenuse² = opposite² + adjacent²
- Positive curvature space: hypotenuse² < opposite² + adjacent²
- Negative curvature space: hypotenuse² > opposite² + adjacent²
Hyperbolic Geometry
Can we have a surface, with a constant negative curvature everywhere, in the same way that a sphere has a constant positive curvature everywhere?
see hyperbolic geometry.


