I don't even know if anyone has worked out a model for homotopy type theory so this is not a serous attempt to implement HoTT in Idris. I am just trying to work through a simple example to try to get a feel for what the issues might be.
| To get the simplest interesting type, start with a boolean type. |
|
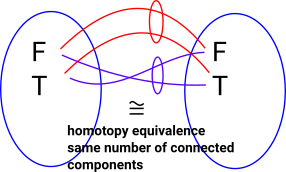 |
There are two ways for terms of this type to be 'equal'. We could match T to T and F to F or T to F and F to T. |
| So here I have implemented these two 'equalities' as Id1 and Id2: |
data Id1 : MyBool -> MyBool -> Type where
Refl11 : Id1 T T
Refl12 : Id1 F F
data Id2 : MyBool -> MyBool -> Type where
Refl21 : Id2 T F
Refl22 : Id2 F T |
|
These two equalities are not homotopically equivalent to each other because one cannot be continuously deformed into the other.
| So we can now think about possible higher order equivalences between the equivalences. |
data IdId : a -> b -> Type where
Refl1' : IdId Id1 Id1
Refl2' : IdId Id2 Id1
Refl3' : IdId Id1 Id2
Refl4' : IdId Id2 Id2 |
|
