On the previous page we saw that, in a plane, expressions that involve points and lines can be rewritten in a way that points and lines are interchanged, for instance:
- Two lines define (meet at) a point.
- Two points define (joint to make) a line.
This can also apply to certain finite subsets of a plane, for example the fano plane, this consists only 7 points and 7 lines. Although each line contains 3 points it takes only 2 points to define the line also although each line is crossed by 3 lines it only takes 2 lines to define the point.
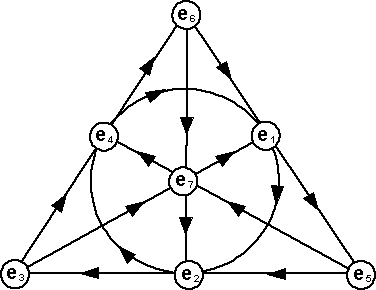
We can see that one of the lines is a circle rather than being a straight line. We could consider the points on this line (e1, e2 and e4) to be at infinity and then we could consider the line straight.
One of the applications of the fano plane is to help us define the multiplication rules for octonions as explained here.
Are there any other subsets of the plane which have this duality? Well a simple case would be a triangle:
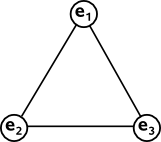
We can easily see that any two points define a line and any two lines define a point.
What about a figure with 4 points and 4 lines?
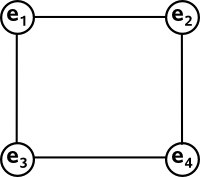
In this case the points diagonally opposite each other don't define a line and the parallel lines don't meet and so don't define a pont, so this does not have the duality required.
In fact we cant have any parallel lines (unless we include a point on the line at infinity) because, if the two lines don't meet, they can't define a point.
This tends to indicate that our plane must be an elliptical geometry (which has no parallel lines as explained here) or we might use the more general case of projective geometry (as explained here).
So far we have two cases, the triangle where:
- there are 3 points
- there are 3 lines
- each line contains 2 points.
- each point is crossed by 2 lines.
and we have the fano plane where:
- there are 7 points
- there are 7 lines
- each line contains 3 points.
- each point is crossed by 3 lines.
So we might expect the next case in this sequence to be:
- there are 15 points
- there are 15 lines
- each line contains 4 points.
- each point is crossed by 4 lines.
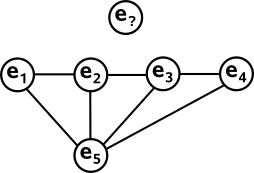
But does such a construction exist? Its easy to construct the first line with 4 points on it (e1, e2, e3 and e4) and we can add points (e5) with 4 lines through it. But how do we go on to meet the requirements? I'm not sure how to proceed.