Maths - Factoring Groups

On the previous pages we saw how to combine two or more groups into a bigger group, here we look at the reverse process, that is, breaking a group down into two or more simpler groups.

Lets assume that we have a group G and we have a subgroup of G which we call N. We want to find the other subgroup G/N. For G/N to be a group then N must be a normal subgroup.

Test that N is a normal subgroup

To test that N is a normal subgroup then:

x N x^-1 must be a member of N for every x in G

Calculation of G/N

we calculate the set:

aN | aG

This will be the group G/N under the operation

(a N) (b N) = a b N

Example 1 - divide C by Z₂

G = Complex numbers = C

N = Z₂

Test for Normal Subgroup

x	x N x-1
1	1 {1,-1} 1 = {1,-1}
-1	-1 {1,-1} -1 = {1,-1}
i	i {1,-1} -i = {1,-1}
-i	-i {1,-1} i = {1,-1}

So x N x^-1 is a member of N for every x which means that G/N will be a group and we can go on to calculate it.

Calculation of G/N

Elements of G/N are a•N:

1•{1,-1} = {1,-1}
-1•{1,-1} = {-1,1}
i•{1,-1} = {i,-i}
-i•{1,-1} = {-i,i}

so the elements are:

{1,-1} and {i,-i}

Example 2 divide H by C

G is the group of quaternions H:

Cayley Table	Cayley Graph
a*b b.1 b.i b.j b.k a.1 1 i j k a.i i -1 k -j a.j j -k -1 i a.k k j -i -1

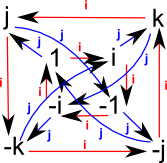Note: in this example I have not shown the negative elements so where i is shown we also have -i and so on for the other elements.

We want to divide it by C to get H/C

Test for Normal Subgroup

x	x K x-1
1	1 {1,i} 1 = {1,i}
i	i {1,i} -i = {-1,-i}
j	j {1,i} -j = {-1,-i}
k	k {1,i} -k = {-1,-i}

So x K x^-1 is a member of K for every x which means that G/K will be a group and we can go on to calculate it.

Calculation of G/N

Elements of G/N are a•N:

1•{1,i} = {1,i}
i•{1,i} = {-1,i}
j•{1,i} = {j,-k}
k•{1,i} = {k,-j}

So the elements are:

{±1,±i} and {±j,±k}

which gives the multipication table:

a*b	{±1,±i}	{±j,±k}
{±1,±i}	{±1,±i}	{±j,±k}
{±j,±k}	{±j,±k}	{±1,±i}

EuclideanSpace

home

 

Rotating a Cube

Generating Geometric Algebras