Maths - Functor Covarient and Contravarient

Covarient and Contravarient Functors

There are two ways that a given morphism can preserve structure:

This is the covarient case where the start of the arrow in C maps to the start of the arrow in D and the end of the arrow in C maps to the end of the arrow in D.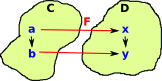
This is the contravarient case where the start of the arrow in C maps to the end of the arrow in D and the end of the arrow in C maps to the start of the arrow in D.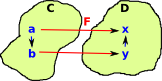

	Unless otherwise stated we usually assume that a morphism/functor is covarient so we can draw this as on the left.
	For the contravarient case we could invent some sort of special symbol for a contravarient morphism/functor. However is usually easier to reverse the internal arrows in either C or D. On the left we have reversed C by making it C^op. So now we can use an ordinary arrow between C and D.

The way that covarient and contravarient functors arise, in this case, is as follows.

Let 'A', 'X' and 'Y' be elements of a class 'C'. let 'f' be a functor from 'X' to 'Y'. Assume that both 'A' and 'f' are fixed:

covarient	contravarient

If 'f' and 'h' are known then we can derive 'g' (by composition) If 'f' and 'g' are known then we cannot derive 'h' (see concepts of section and retraction). So given some fixed 'f' the 'g' depends on 'h' which I have drawn below as an arrow between arrows.	If 'f' and 'g' are known then we can derive 'h' (by composition) If 'f' and 'h' are known then we cannot derive 'g' (see concepts of section and retraction). So given some fixed 'f' the 'h' depends on 'g' which I have drawn below as an arrow between arrows.

This arrow goes in the same direction to f, hence it is covarient.	This arrow goes in the opposite direction to f, hence it is contravarient.

We now need to combine these ideas with the concept of hom sets as follows.