Group Theory
In order to represent rotations we only need a subset of quaternion algebra, that is, we only need quaternions with the multiplication operation. this forms a group.
Quaternions and SU(2)
A group can be defined by its Cayley table but since we are not using addition (or its inverse - subtraction) we cant take negative values.
| a*b | b.1 | b.i | b.j | b.k |
| a.1 | 1 | i | j | k |
| a.i | i | -1 | k | -j |
| a.j | j | -k | -1 | i |
| a.k | k | j | -i | -1 |
We can fix this by making the minus values elements of the group:
Cayley Table |
Cayley Graph |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
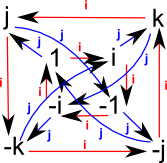 |
This gives a group containing 8 elements. The group can be 'generated' from 2 elements, that is, if we start from the identity element and apply a sequence of the generators (say 'i' and 'j') we can get to any element.
Since we now have an abstract group we can give the elements any name we want, the following is often used as it gives the elements in terms of two generators 'a' and 'b'.
Cayley Table |
Cayley Graph |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
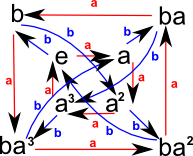 |
Rotation Group and Reflection Group
We apply the transform by using the 'sandwich product'.
- Can we represent this 'sandwich product' as a single binary operation.
- How do 3D reflections and 3D rotations interact?
When we are trying to understand a difficult problem (3D reflections and rotations are difficult for me) it often helps to solve a simpler but related problem.
So instead of infinite groups such as SU(2) groups explained here. Let us consider a finite group, the dihedral group (see this page) -.
Let this finite group contain the following operations:
1) reflection in the x axis (y,z plane) x › -x
2) reflection in the y axis (x,z plane) y › -y
3) reflection in the z axis (x,y plane) z › -z
This group is not yet closed we need to consider the following combinations:
4) reflection in the x axis followed by reflection in the y axis ( x › -x , y › -y) this is equivalent to a rotation of 180 degrees about the z axis.
5) reflection in the z axis followed by reflection in the x axis ( z › -z , x › -x) this is equivalent to a rotation of 180 degrees about the y axis.
6) reflection in the y axis followed by reflection in the z axis ( y › -y , z › -z) this is equivalent to a rotation of 180 degrees about the x axis.
There is one final combination:
7) reflection in all 3 axies ( x › -x , y › -y, z › -z), this is a combination of a reflection and a rotation, it is like a reflection through a point rather than through a plane. What would we call such an operation - a rotflection?
Together with the identity element this gives us 8 operations:
| description | transform | quaternion representation | |
|---|---|---|---|
| 0 | identity | x › x , y › y, z › z | p' = 1 * p * 1 |
| 1 | reflection in the x axis | x › -x , y › y, z › z | p' = i * p * i |
| 2 | reflection in the y axis | x › x , y › -y, z › z | p' = j * p * j |
| 3 | reflection in the z axis | x › x , y › y, z › -z | p' = k * p * k |
| 4 | rotation of 180 degrees about the z axis | x › -x , y › -y, z › z | p' = i * j * p * j * i p' = k * p *-k |
| 5 | rotation of 180 degrees about the y axis | x › -x , y › y, z › -z | p' = i * k * p * k * i p' = j * p *-j |
| 6 | rotation of 180 degrees about the x axis | x › x , y › -y, z › -z | p' = j * k * p * k * j p' = i * p *-i |
| 7 | reflection through origin point | x › -x , y › -y, z › -z | p' = i * j * k * p * k * j * i |
Note 1: inverting one axis produces a reflection in a plane, inverting two axies produces a rotation through 180 degrees, inverting 3 axies produces a reflection through a point.
Note 2: the quaternion representation either has the form p' = q * p * q for reflections or p' = q * p * -q for rotations.
Note 3: two reflections are combined by wrapping one round the other. For example, reflecting in x axis is:
p' = i * p * i
Then to reflect this result in the y axis, we wrap the whole result in j which gives:
p' = j * i * p * i * j
Note 4: although reflecting in x axis is given a quaternion representation of p' = i * p * i it could just as well have used the representation p' = -i * p * -i. In other words inverting poth the pre and post quaternion has no effect, so I have not included both options.
Combining these 8 elements
This table fully defines how these operations combine:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 0 | 4 | 5 | 2 | 3 | 7 | 6 |
| 2 | 2 | 4 | 0 | 6 | 1 | 7 | 3 | 5 |
| 3 | 3 | 5 | 6 | 0 | 7 | 1 | 2 | 4 |
| 4 | 4 | 2 | 1 | 7 | 0 | 6 | 5 | 3 |
| 5 | 5 | 3 | 7 | 1 | 6 | 0 | 4 | 2 |
| 6 | 6 | 7 | 3 | 2 | 5 | 4 | 0 | 1 |
| 7 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
We can replace the operation number in the table entry to give the quaternion representation:
| 1 | i | j | k | -k | -j | -i | -1 | |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | i | j | k | -k | -j | -i | -1 |
| i | i | 1 | -k | -j | j | k | -1 | -i |
| j | j | -k | 1 | -i | i | -1 | k | -j |
| k | k | -j | -i | 1 | -1 | i | j | -k |
| -k | -k | j | i | -1 | 1 | -i | -j | k |
| -j | -j | k | -1 | i | -i | 1 | -k | j |
| -i | -i | -1 | k | j | -j | -k | 1 | i |
| -1 | -1 | -i | -j | -k | k | j | i | 1 |
Note 1: this is a special notation, a negative sign indicates inversion (conjugation) of the second quaternion only. i.e.
plus sign: p' = q * p * q
negative sign: p' = q * p * -q
Question: is there such a concept of 'spinorial reflections'? What could this mean?
This is a 'double cover' of reflections in that '-i' produces the same reflection as 'i'. However, I cant find an equivalent to rotations, where rotation of 360 degrees swaps between the two forms. Two reflections always produce identity or a rotation. Combining a reflection and a rotation will produce another reflection so perhaps this will swap between the two forms?
Perhaps this idea only applies to continuous groups where a rotation through 360 degrees is a continuous movement on the surface of a manifold, this cant really apply to a finite group like this, which only involves jumps from one position to another. But reflections are always jumps aren't they?
Warning
This is a very special case, it is not a multiplication table for i,j & k
For example , rotations should anti-commute?
so i * j * p * -j * -i
rotates in the opposite direction to:
j * i * p * -i * -j
This is a special case because these rotations are only 180 degrees, which just happens to be the same as its inverse, but this is generally not the case.
So be careful not to learn the wrong lessons for continuous rotations.
More General Group
The above group does not cover the full properties of rotations, especially the anti-commute properties, we can therefore expand the group to make a larger superset of the finite group.
I guess what I'm trying to aim for is a set of 'base' operations where we could combine them by some function, in a lie group sort of way, to give a the full continuous 'infinite' group of reflections and rotations in 3D. I don't know if this is possible?
So, to expand the group, we add reflections in a plane at 45deg to two primary axes, and any other transforms these generate. These reflections are equivalent to swapping two axies. So we want to have a table of operations that has every combination of inverting and swapping axies.
I am still working on this table, there are a lot more entries that need to be added
| description | transform | quaternion representation | |
|---|---|---|---|
| 0 | identity | x › x , y › y, z › z | p' = 1 * p * 1 |
| 1 | reflection in the x axis | x › -x , y › y, z › z | p' = i * p * i |
| 2 | reflection in the y axis | x › x , y › -y, z › z | p' = j * p * j |
| 3 | reflection in the z axis | x › x , y › y, z › -z | p' = k * p * k |
| 4 | reflection in 45deg to x & y | x › y , y › x, z › z | p' = (0.7071 i + 0.7071 j) * p * (0.7071 i + 0.7071 j) |
| 5 | reflection in 45deg to y & z | x › x , y › z, z › y | p' = (0.7071 j + 0.7071 k) * p * (0.7071 j + 0.7071 k) |
| 6 | reflection in 45deg to x & z | x › z , y › y, z › x | p' = (0.7071 i + 0.7071 k) * p * (0.7071 i + 0.7071 k) |
| 7 | reflection in -45deg to x & y | x › y , y › -x, z › z | p' = (0.7071 i - 0.7071 j) * p * (0.7071 i - 0.7071 j) |
| 8 | reflection in -45deg to y & z | x › x , y › z, z › -y | p' = (0.7071 j - 0.7071 k) * p * (0.7071 j - 0.7071 k) |
| 9 | reflection in -45deg to x & z | x › z , y › y, z › -x | p' = (0.7071 i - 0.7071 k) * p * (0.7071 i - 0.7071 k) |
| 7 | rotation of 180 degrees about the z axis | x › -x , y › -y, z › z | p' = i * j * p * j * i p' = k * p *-k |
| 8 | rotation of 180 degrees about the y axis | x › -x , y › y, z › -z | p' = i * k * p * k * i p' = j * p *-j |
| 9 | rotation of 180 degrees about the x axis | x › x , y › -y, z › -z | p' = j * k * p * k * j p' = i * p *-i |
| 7 | reflection through origin point | x › -x , y › -y, z › -z | p' = i * j * k * p * k * j * i |
Generating a Quaternion Group using a Program
We can use a computer program to generate these groups, here I have used Axiom/FriCAS which is described here.
e1:SquareMatrix(2,Complex Fraction Integer) := squareMatrix[[0,1],[1,0]]
Type: SquareMatrix(2,Complex(Fraction(Integer)))
e2:SquareMatrix(2,Complex Fraction Integer) := squareMatrix[[0,-%i],[%i,0]]
Type: SquareMatrix(2,Complex(Fraction(Integer)))
e3:SquareMatrix(2,Complex Fraction Integer) := squareMatrix[[1,0],[0,-1]]
Type: SquareMatrix(2,Complex(Fraction(Integer)))
i := e1*e2
Type: SquareMatrix(2,Complex(Fraction(Integer)))
j := e2*e3
Type: SquareMatrix(2,Complex(Fraction(Integer)))
k := e3*e1
Type: SquareMatrix(2,Complex(Fraction(Integer)))
PM := PauliMatrix(2,false,3,Complex Fraction Integer,[e1,e2,e3])
Type: Type
(8) -> toTable()$PM
Type: Matrix(PauliMatrix(2,false,3,Complex(Fraction(Integer)),
[MATRIX,MATRIX,MATRIX]))
(9) -> |