The dual of a complex number, dual complex numbers are 4 dimensional elements, these dimensions are:
- 1 = a real dimension.
- i = an imaginary dimension.
- ε = a dimension which squares to zero.
- iε = also squares to zero and anti commutes with ε.
The usual Addition and subtraction rules apply, just add corresponding terms, the interesting properties are defined by the multiplication table:
a*b |
b.1 | b.i | b.ε | b.iε |
| a.1 | 1 | i | ε | iε |
| a.i | i | -1 | iε | -ε |
| a.ε | ε | -iε | 0 | 0 |
| a.iε | iε | ε | 0 | 0 |
Representing Transforms
This can be used to represent the group of spatial displacements in two dimensions SE(2) which can be used to represent a combination of 2D rotation and displacement.
The advantage of this is that we can represent a combined rotation with displacement operation with one multiplication operation.
- The 1 and i terms together can represent rotation (as a normalised complex number).
- The ε and iε terms together can represent displacement.
In order to investigate the practicality of this we can try to use it in the car racing game (which is developed on these pages). This is used in the following examples:
Example - Pure Displacement (no rotation)
If the rotation is 0 degrees, this is represented by (1 + 0 i), in other words 1, as explained on this page.
So if we are initially at point (x=3, y=4) this will be represented by the Dual Complex Number:
(1 + 3ε + 4 iε)
We now want to displace this by (x=4, y=3) this will be represented by the Dual Complex Number:
(1 + 4ε + 3 iε)
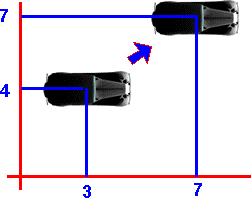
So to combine these, to give the resulting position, we multiply together their representations:
(1 + 3ε + 4 iε)*(1 + 4ε + 3 iε)
multiplying out the terms using the above multiplication table we get:
= 1 + 4ε + 3 iε + 3ε + 4 iε
= 1 + 7ε + 7 iε
Example - Pure Rotation (no displacement)
If the displacement is zero then ε = 0 and iε =0 and the rotation is represented by the normalised complex number as explained on this page.
Example - Combined Displacement and Rotation
Starting from the previous position:
(1 + 7ε + 7 iε)
and applying a rotation of 90 represented by:
(0 + i)
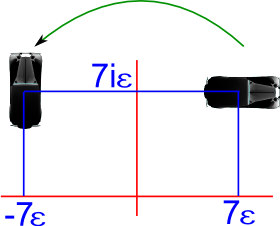
We combine them by multiplying as before:
(0 + i)*(1 + 7ε + 7 iε)
Note: the rotation (or whatever translation we are using) is the first operand in the multiplication, if we reverse the order the rotation will go in the wrong direction.
Multiplying out the terms using the above multiplication table we get:
(i + 7 iε - 7 ε)
So we can see that the object is rotated about the origin.
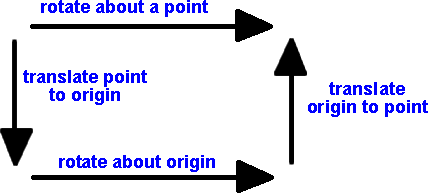
Rotation about a point
In the above we are rotating about the origin. This is sometimes what we want to do, for instance, if we are observing the world from the frame of reference of a car and we assume it to be at the origin then, when it turns, the other cars will appear to rotate round it. If we want a car to rotate about its own centre then we can just multiply the complex number part (1 and i) and ignore the ε and iε part.
If we want to rotate about an arbitrary point then we first translate this point to the origin, then rotate about the origin, then translate the origin back to the point (as discussed on this page).
Inverse of dual quaternion
Due to the zero terms in the multiplication table I don't think there is a general multiplicative inverse because information is lost by multiplication.
However, if we restrict ourselves to the linear rotation-displacement discussed above, then there must be an inverse because the operations they represent have an inverse. The complex number is always normalised so its inverse will be its conjugate and the inverse of the displacement is minus its value.
So, in this case, the inverse of:
a + b i + c ε + d iε
is:
a - b i - c ε - d iε
Spinor-like form
As with pure complex number translations we can pre and post-multiply by half the rotation, in the above example this would give:
(0.701 + i 0.701) * (1 + 7ε + 7 iε) * (0.701 + i 0.701)
=(0.701 + i 0.701) * (0.701 + i 0.701 + 9.9 ε)
=(i + 7 ε + 7 iε)
Equivalence to Geometric Algebra
This is equivalent to the Geometric Algebra G 1,1,0 as described on this page.
where the following are equivalent:
| dual complex | G 1,1,0 |
| 1 | e |
| i | e1 |
| ε | a.e2 |
| iε | a.e12 |
The use of Geometric Algebra to represent this type of tranform can be analysed using conformal space as described on this page.
Further Reading
- Dual Quaternions - for 3 dimentional translations
- Clifford / Geometric Algebra - for a more theortical approach

