Maths - clifford / Geometric Algebra - Geometrical Interpretation

Scalar

This can represent a dimensionless quantity, such as energy for instance.

In the class definition (here) I have used the variable 'e' to represent the scalar part of the multivector.

Vector

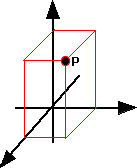
A 3D vector can represent a direction element such as a point in 3d space relative to the origin of the coordinate system or say, a movement within the coordinate system.

The 3D can be represented as a linear combination of 3 basis:

e₁
e₂
e₃

These basis don't have to be mutually perpendicular (although for the practical applications of this program they probably will be) however they do have to be independent of each other, in other words they should not be parallel to each other and all 3 should not be in the same plane.

In the class definition (here) I have used the variables 'e1', 'e2' and 'e3' to represent the vector value of the multivector.

So the vector can be represented by:

e1 e₁ + e2 e₂ + e3 e₃

BiVector

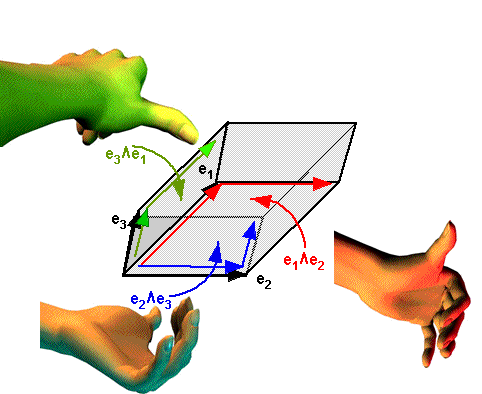
This can represent a plane element or area element. As shown here a plane can also represent a direction of rotation in 3D.

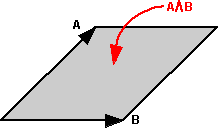
So in 3 dimensions there are 3 BiVectors for any gives set of bases, represented by the 3 possible pairings of the bases. Each of these BiVectors, for example e₁ ^ e₂, represents the area in the plane of these vectors. This area will be maximum when A and B are at 90 degrees (right angles) to each other and zero when the vectors are along the same line (not allowed for basis vectors). Note also that this area is signed, that is, it may be negative. It will be reversed if the order is changed e₁ ^ e₂ = -e₂ ^ e₁.

So the three BiVectors are:

e₁ ^ e₂
e₃ ^ e₁
e₂ ^ e₃

Where:

^ = outer product operator (for more information about multivector arithmetic see here)

These 3 BiVectors are not vectors, but they can be represented by a vector, by finding a vector which is mutually perpendicular to the 2 vectors which make up the BiVector. This is the same as the 'x' cross product since we are working in 3D here.

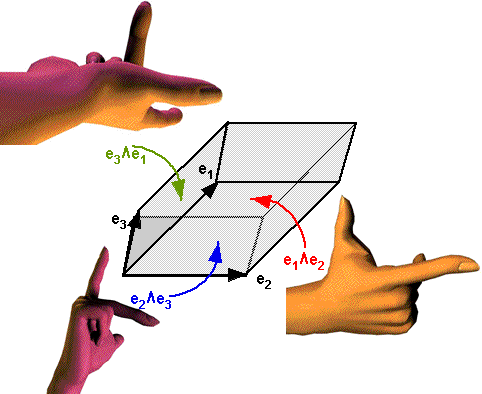
In the diagram above I have shown an equivalent direction being found by left or right hand rule. The first finger gives the direction of the vector before the ^, the second finger gives the direction of the vector after the ^, the thumb will then give the direction of the equivalent vector. However, this may be positive or negative as explained above, so we may need to invert the direction depending on the order of the operands.

So how do we choose the order of the vectors in the bivector? In other words why did we choose these bivectors:

e₁ ^ e₂
e₃ ^ e₁
e₂ ^ e₃

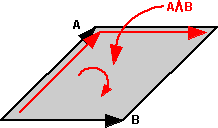
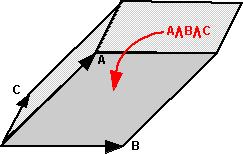
In his book, David Hestines associates bivectors with a rotation as shown above, because the order is A^B this gives a clockwise rotation on the diagram. Using this rotation concept it is much easier to explain how a bivector can be negative than only describing it as an area.

The diagram below shows the rotations associated with all 3 bivectors:

So can we use this to choose the order of bases in the bivectors? If, using the left hand, we curl the fingers in the direction of the rotation then, the thumb seems to point in the direction of the other vector (at least in the way I've drawn it here). Can anyone think of a way that this idea could be generalised?

In the class definition (here) I have used the variables 'exy', 'ezx' and 'eyz' to represent the bivector value of the multivector.

So the vector can be represented by:

e₁ ^ e₂ exy + e₃ ^ e₁ ezx + e₂ ^ e₃ eyz

TriVector

This can represent a volume element. Also known as a pseudoscalar = square root of -1

e₁ ^ e₂ ^ e₃

exyz

exyz e₁ ^ e₂ ^ e₃

The TriVector is very similar to the determinant of a 3x3 matrix made up of the three vectors a,b and c as described here.

Multivector

So the 3D multivector consists of the following variables

Interpretation of Inner and Outer Products

The inner and outer products can be related to a plane in 'n' dimensional space. Related pages:

• Discussion about planes in 'n' dimentional space.
• Discussion about projections on planes.

The inner and outer products can represent the perpendicular and parrallel components to a plane as follows:

Parallel Component of a Point

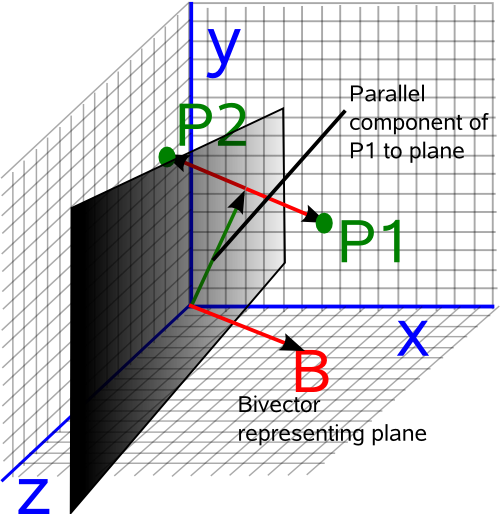
The parallel component is denoted as follows:

A || B = (A•B) B^-1

Where:

• A = vector representing a point to be transformed
• B = bivector representing the plane.
• • = inner product (vector dot product)

But we know from Geometric Algebra (GA arithmetic) that,

a•K = ½ (aK + (-1)^k+1Ka)

where:

• K = a mulivector of grade 'k'
• k = grade of multvector

Since, in this case, K is a bivector then we will denote it by B and set k=2.

A•B = ½ (AB + BA)

So substituting in the above equation gives:

A || B = ½ (AB + BA) B^-1

A || B = ½ (A + BAB^-1)

Discussion of this in 3D using quaternions.

Perpendicular Component of a Point

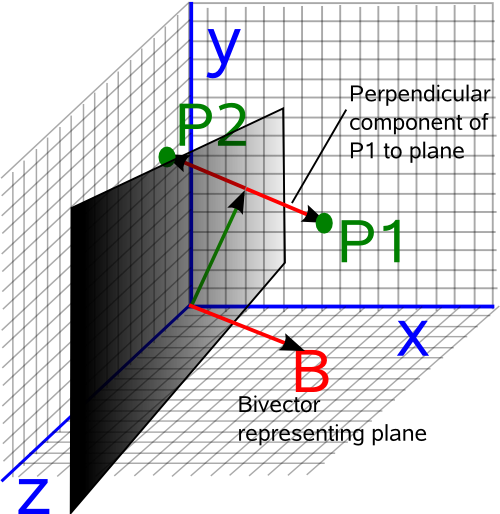
The perpendicular component is denoted as follows:

A B = (A ^ B) B^-1

• A = vector representing a point to be transformed
• B = bivector representing the plane.
• ^ outer product (in this 3D case equivalent to × vector cross product)

But we know from Geometric algebra that,

a^K = ½ (aK + (-1)^k Ka)

where:

• K = a mulivector of grade 'k'
• k = grade of multvector

Since, in this case, K is a bivector then we will denote it by B and set k=2.

A^B = ½ (AB - BA)

So substituting in the above equation gives:

A B = ½ (AB - BA) B^-1

A B = ½ (A - BAB^-1)

Converting this to quaternion terminology gives:

Pout = ½ Pin - q * Pin * conj(q)

but in this case the real part of q is zero (unlike quaternions representing rotations) therefore: conj(q) = -q

So we have:

Pout = ½ Pin + q * Pin * q

Discussion of this in 3D using quaternions.

Reflection in a Plane

From the above diagrams we can see that:

P1 = (P1 || B) + (P1 B)

In other words the parallel component plus the perpendicular component is the point itself.

However to get the point reflected in the plane (P2) we keep the parallel component the same but invert the perendicular component:

P2 = (P1 || B) - (P1 B)

P2 = (P1•B) B^-1 - (P1 ^ B) B^-1

P2 = ((P1•B) - (P1 ^ B)) B^-1

Since the inner product commutes in 3D and the outer product anticommutes we get:

P2 = ((B•P1) + (B^P1)) B^-1

We know from Geometric Algebra that the geometric product is the sum of the inner and outer products:

B A = B•A + B^A

so we get:

P2 = B P1 B^-1

Discussion of this in 3D using quaternions.

EuclideanSpace

home

Transforms

Projections

Directed Area

Screw Theory