Maths - 4D Clifford / Geometric Algebra

Prerequisites

If you are not familiar with vectors this subject you may like to look at the following page first:

Description

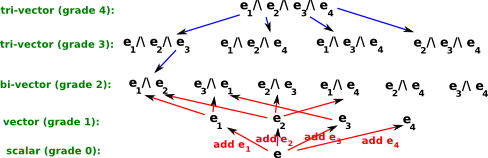
For 4 dimensions can be generated by 4 basis vectors, e₁, e₂, e₃ and e₄ this means that a 4D multivector is represented by 16 scalar numbers:

grade diamond

The pages below this explain in detail:

Choice of bivector and tri-vector basis	Here I have described how the order of the indexes was chosen. For instance, why don't we use e214 instead of e124? Unlike 3D multivectors there is no correspondence with cross multiplication as cross multiplication does not apply in 4D. Also I cant work out how to make the multiplication table symmetrical. Also its not possible to make all the e₁₂₃₄ terms on the bottom left to top right diagonal positive as some of these terms anti-commute.
Transform
Arithmetic	This gives the rules for addition, subtraction and multiplication of 4D multivectors.
Functions	This shows the dual, reverse and conjugate functions of of 4D multivectors.
isometries
code
pauli	An alternative notation using a matrix to represent each multvector

The following table explains the notation for each of the 16 elements as follows:

grade	base value		numerical value
grade	full	shortened	numerical value
0=unit scalar	1		e
1=unit length base vectors	e₁		e1
	e₂		e2
	e₃		e3
	e₄		e4
2=unit length base bivectors	e₁^ e₂	e₁₂	e12
	e₁^ e₃	e₁₃	e13
	e₁^ e₄	e₁₄	e14
	e₂^ e₃	e₂₃	e23
	e₄^ e₂	e₄₂	e42
	e₃^ e₄	e₃₄	e34
3=unit length base tri-vector	e₃^ e₂^ e₁	e₃₂₁	e321
	e₁^ e₂^ e₄	e₁₂₄	e124
	e₄^ e₃^ e₁	e₄₃₁	e431
	e₂^ e₃^ e₄	e₂₃₄	e234
4=unit length base tri-vector	e₁^ e₂^ e₃^ e₄	e₁₂₃₄	e1234

So in this case the number of dimensions is:

scalar dimensions=1
vector dimensions=4
bivector dimensions=6
tri-vector dimensions=4
quad-vector dimensions=1

In this case the number of scalar values in the multivector is 16 = (1+4+6+4+1)

metadata block

see also:

newsgroup discussion

Correspondence about this page

Book Shop - Further reading.

Where I can, I have put links to Amazon for books that are relevant to the subject, click on the appropriate country flag to get more details of the book or to buy it from them.

Geometric Computing for Perception Action Systems: Concepts, Algorithms, and Scientific Applications (Hardcover). This is the only book I have so far come across that has a reasonable explanation of 'motors' and why it is useful to use 4D Geometric algebra to represent kinematics of solid bodies (in chapter 2). The book is quite a slim volume considering that it covers both fundamental concepts and practical applications. Therefore I think you will need to have a good understanding of Geometric Algebra before starting on this book.

Commercial Software Shop

Where I can, I have put links to Amazon for commercial software, not directly related to the software project, but related to the subject being discussed, click on the appropriate country flag to get more details of the software or to buy it from them.

Mathmatica

Can you help?

Please send me any improvements to here. I would appreciate ideas to make the pages more useful including error correction, ideas for new pages, improvements to wording. It helps if you quote the full URL of the page.

Could anyone let me know of a good proof that a quaternion multiplication can be used to represent a rotation in 3 dimensions, I'm not looking for the shortest proof, but the most easily understood.

Terminology and Notation

Specific to this page here:

program

I am working on a project which uses these principles, if you would like to help me with this you are welcome to join in, here:

http://sourceforge.net/projects/mjbworld/

This site may have errors. Don't use for critical systems.