Rotation
So why do we use an equation like: Pout = q * Pin * conj(q) to rotate a point?
We can demonstrate it works by expanding out the parts of the complex number using:
- Pout = i Pout.x + j Pout.y + k Pout.z
- q = qw + i qx + j qy + k qz
- Pin = i x + j y + k z
So using the above equation and expanding out the terms gives:
Pout.x = x*(qx*qx+qw*qw-qy*qy- qz*qz) + y*(2*qx*qy- 2*qw*qz) + z*(2*qx*qz+ 2*qw*qy)
Pout.y = x*(2*qw*qz + 2*qx*qy) + y*(qw*qw - qx*qx+ qy*qy - qz*qz)+ z*(-2*qw*qx+
2*qy*qz)
Pout.z = x*(-2*qw*qy+ 2*qx*qz) + y*(2*qw*qx+ 2*qy*qz)+ z*(qw*qw - qx*qx- qy*qy+
qz*qz)
The full working is shown on this page, its hard to see whats happening here so it may help to show the same equations in the form of a matrix:
We can compare this with other matrix forms for rotation and therefore convince ourselves that this represents a rotation.
However, although this shows that the equation gives the result we want, it does not really explain why the equation is in this form.
We can try doing the same expansion but using the scalar and vector notation as shown on this page.
Reflection and Projections
We can use the Geometric Algebra inner and outer product to represent the perpendicular and parrallel components to a plane as follows:
Parallel Component of a Point
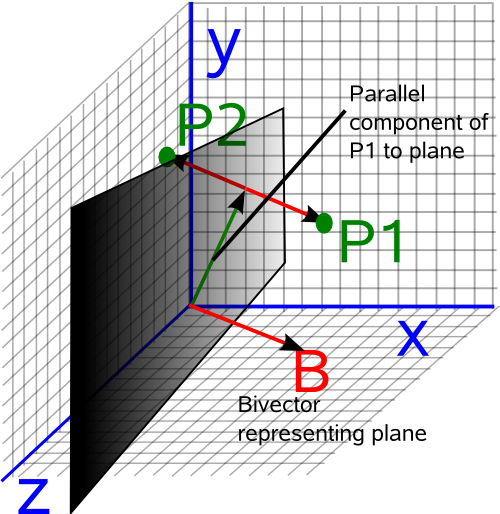
The parallel component is denoted as follows:
A || B = (A•B) B-1
Where:
- A = vector representing a point to be transformed
- B = vector representing the plane.
- • = vector dot product
But we know from Geometric algebra that,
A•B = ½ (AB + BA)
So substituting in the above equation gives:
A || B = ½ (AB + BA) B-1
A || B = ½ (A + BAB-1)
Converting this to quaternion terminology gives:
Pout = ½ Pin + q * Pin * conj(q)
but in this case the real part of q is zero (unlike quaternions representing rotations) therefore: conj(q) = -q
So we have:
Pout = ½ Pin - q * Pin * q
Perpendicular Component of a Point
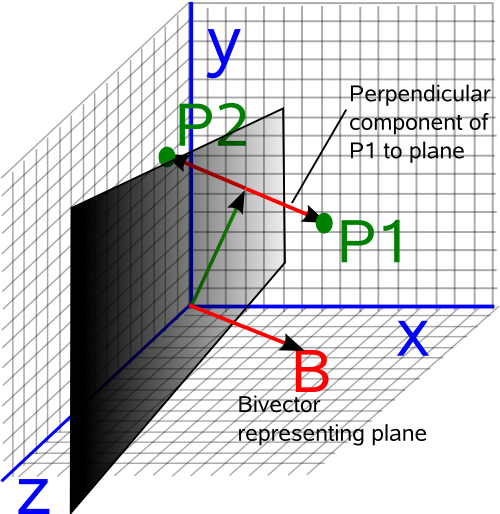
The perpendicular component is denoted as follows:
A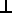 
B = (A ^ B) B-1
- A = vector representing a point to be transformed
- B = vector representing the plane.
- ^ outer product (in this 3D case equivalent to × vector cross product)
But we know from Geometric algebra that,
A^B = ½ (AB - BA)
So substituting in the above equation gives:
A 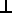B = ½ (AB - BA) B-1
A 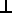B = ½ (A - BAB-1)
Converting this to quaternion terminology gives:
Pout = ½ Pin - q * Pin * conj(q)
but in this case the real part of q is zero (unlike quaternions representing rotations) therefore: conj(q) = -q
So we have:
Pout = ½ Pin + q * Pin * q
Reflection in a Plane
From the above diagrams we can see that:
P1 = (P1 || B) + (P1 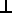B)
In other words the parallel component plus the perpendicular component is the point itself.
However to get the point reflected in the plane (P2) we keep the parallel component the same but invert the perendicular component:
P2 = (P1 || B) - (P1 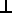B)
P2 = (P1•B) B-1 - (P1 ^ B) B-1
P2 = ((P1•B) - (P1 ^ B)) B-1
Since the inner product commutes in 3D and the outer product anticommutes we get:
P2 = ((B•P1) + (B^P1)) B-1
We know from Geometric Algebra that the geometric product is the sum of the inner and outer products:
B A = B•A + B^A
so we get:
P2 = B P1 B-1
Converting this to quaternion terminology gives:
Pout = q * Pin * conj(q)
since conj(q) = -q we get:
Pout = - q * Pin * q
