In order to work with rotations using the multiplication operator, in particular to combine two individual rotations to give an equivalent single rotation, then we need to use the even sub-algebra.
Complex Numbers
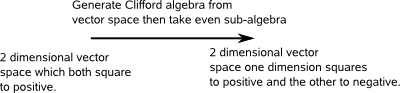
So if we start with 2D euclidean space, that is two dimensions that both square to positive, then we get the Clifford algebra G 2,0,0:
e = scalar (squares to positive)
e1 = vector (squares to positive)
e2 = vector (squares to positive)
e12 = bivector (squares to negative)
Taking the even sub-algebra we take just the scalar and bivector dimensions:
e = scalar (squares to positive)
e12 = bivector (squares to negative)
This is equivalent (isomorphic to) complex number algebra.
Double Numbers
This time we start with a vector space where one dimension squares to positive and the other squares to negative, then we get the Clifford algebra G 1,1,0:
e = scalar (squares to positive)
e1 = vector (squares to positive)
e2 = vector (squares to negative)
e12 = bivector (squares to positive)
Taking the even sub-algebra we take just the scalar and bivector dimensions:
e = scalar (squares to positive)
e12 = bivector (squares to positive)
This is equivalent (isomorphic to) double number algebra.
Duality
So, from the above, there appears to be a duality between Euclidean and Minkowski space, where rotations in Euclidean space are calculated using Minkowski space and visa versa.

