In addition to full 3D views with perspective projections the program also has simpler 2D windows using Orthographic projection. This is to allow CAD type applications and applications where full 3D rendering is not required or is not supported.
To do this we need to represent 3D shapes, such as a cylinder, by using 2D shapes such as ellipse and lines.
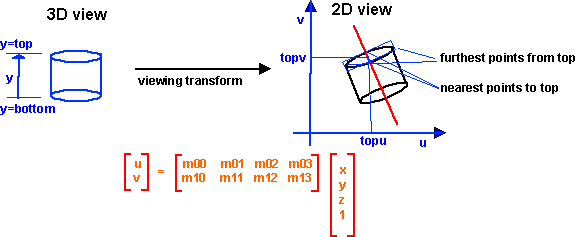
We want to find the furthest and nearest points to the translation of the top to the 2D plane.
So we need to find the minima and maxima of:
f = (v - topv)
+(u - topu)
subject to the constraint that:
g(u,v) = x+z-
r= 0
we also know
u = m00 x + m01 y + m02 z + m03
v = m10 x + m11 y + m12 z + m13
g / u
= ( g / x
)( x / u
) + ( g / y
)( y / u
)
g / v
= ( g / x
)( x / v
) + ( g / y
)( y / v
)
sustitute following values in above
g / x
= 2x
g / y
= 2y
x / u
= 1/m00
y / u
= 1/m01
x / v
= 1/m10
y / v
= 1/m11
therefore:
g / u
= 2x / m00 + 2y / m01
g / v
= 2x / m10 + 2y / m11
expanding out f = (v - topv)+(u
- topu) gives:
f = v - 2 v topv + topv)
+ u - 2 u topu + topu)
f / u
= 2u - 2 topu
f / v
= 2v - 2 topv
(2u - 2 topu) = 
(2x / m00 + 2y
/ m01)
(2v - 2 topv) = (2x / m10 + 2y
/ m11)
therefore
-= (u - topu) / (x/m00 + z/m02)
= (v - topv) / (x/m10 + z/m12)
(m00 x + m01 y + m02 z + m03 - topu) * (x/m10 + z/m12) = (m10 x + m11 y + m12 z + m13 - topv) * (x/m00 + z/m02)
(m00/m10) x+ (m02/m10) x z + (
m01 y + m03 - topu)x/m10 + (m00/m12) x z + (m02/m12) z
+ ( m01 y + m03 - topu)z/m12 =
(m10/m00 x + m12/m00 x z + (
m11 y + m13 - topv) x/m00 + m10/m00 x z + m12/m00 z
+ ( m11 y + m13 - topv) z/m02
(m00/m10 - m10/m00) x+ (m02/m10
+ m00/m12 - m12/m00 - m10/m00) x z + ( m01/m10 y + m03/m10 - topu/m10 - m11/m00
y - m13/m00 + topv/m00)x
+ (m02/m12 - m12/m00) z + ( m01/m12
y + m03/m12 - topu/m12 - m11/m02 y - m13/m02 + topv/m02)z =0
combine this with:
x+z=
r
gives
(m00/m10 - m10/m00) x+ (m02/m10
+ m00/m12 - m12/m00 - m10/m00) x sqrt(r-
x) + ( m01/m10 y + m03/m10 - topu/m10
- m11/m00 y - m13/m00 + topv/m00)x
+ (m02/m12 - m12/m00) (r- x)
+ ( m01/m12 y + m03/m12 - topu/m12 - m11/m02 y - m13/m02 + topv/m02)sqrt(r-
x) =0
This is an equation containing x and all the other variables are constants
so in theory its solvable, but I dont know how?
|
Attempt to solve this in terms of u and v, but I don't think this will work becase the 3d to 2d transform is not reversable. constraints: g(u,v) = x where: x = I00 u + I01 v + I02 y = I10 u + I11 v + I12 z = I20 u + I21 v + I22 not sure we can use this? can't derive x,y,z form screen coordinates! g(u,v) = (I00 u + I01 v + I02) expanding gives: g(u,v) = I00 partial differentials are:
using Lagrange 2u - 2 topu + 2 v - 2 topv + divide both sides by 2: u - topu + v - topv + 1/ 1/
( (I00
( (I00
(I00 = (I01
(I00 = u combine with: g(u,v) = I00 gives: I give up |
