Cubical Set - Martin Baker

This page discusses a cubical version of simplicial sets. Simplicial sets are described on the page here.

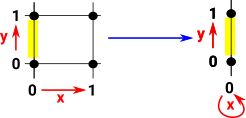
The delta category Δ has:

Objects: The simplicies.
Morphisms: Order preserving injective maps. They embed a face into a larger simplex.

The vertices of the simplicies are ordered by labeling them with natural numbers.

Δ^op has the same objects as Δ but the morphisms are reversed.

The morphisms are now the face maps and degeneracy maps.

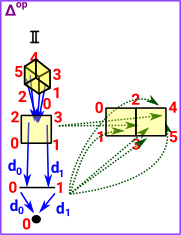Face Maps

These maps go from dimension n+1 dimension n. That is they send a (hyper)cube to one of its faces.

Degeneracy Maps

These maps go in the opposite direction and increase the dimension. That is they add an index.

Order preserving map from simplex to complex:

Gluing

We have a contravarient functor which picks out faces but the faces are not all separate so how do we encode this additional structure?

The edges are connected when they share a common sub-face.

In order to understand this we need the concepts of fibration and lifting as described on the page here.

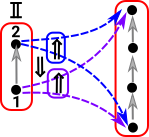
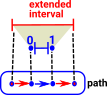
Paths

What happens when there are a sequence of edges following each other? (the target of the first is equal to the source of the second and so on). Can the edge in the interval match the whole path?

Is this the same thing as requiring composition?

In cubical type theory equalities are represented by a path, in a given space, between equal terms.

In order to understand this we need the concepts of cofibration and extentions as described on the page here.

Model Category in CTT

We have some nice properties if mappings are continuous. The most general form of continuous map is mapping between topological spaces where all open sets in codomain have preimage which is an open set. However, lines are not open sets in general. To get these properties we need to restrict to structures where we do have these properties such as maps between simplicies.

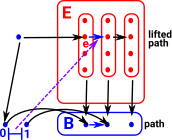
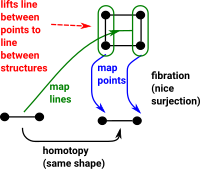
Fibration in CTT

A fibration allows us to 'lift' a line between two points to a line between two structures. This is called the homotopy lifting property (HLP).

In this diagram the blue lines show the mapping of points and the green line maps lines (like open set) in the opposite direction to the points.

Fibrations and HLP are discussed on page here.
CTT is discussed on page here.

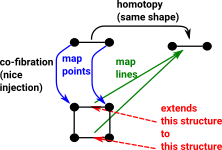
Cofibration in CTT

A cofibration allows us to 'extend' a mapping from a subset to a mapping from the whole structure. This is called the homotopy extension property (HEP).

Again the blue lines show the mapping of points and the green line maps lines (like open set) in the opposite direction to the points.

Cofibrations and HEP are discussed on page here.
CTT is discussed on page here.

Fibration and Co-fibration

Homotopy has the concept of:

a fibration which has the lifting property.
a co-fibration which has the extension property -extension is dual to lift.

	Fibration (lifting property)	Co-fibration (Extension Property)
Homotopy	Fibration (see page here)	Co-fibration (see page here)
Combinatorics (simplicial sets)	Kan fibration (see page here)	Kan extension (see page here)

Kan fibrations are combinatorial analogs of Serre fibrations of topological spaces.

Further Information

Cubical Type theory

Cubical Sets