Simplicial Sets - Sage Code

Sage is mathematical software, it implements simplicial sets as follows:

Sage Code:

• Sage simplicial sets code - topology - definition of AbstractSimplex
  • SimplicialSet_arbitrary at 1095
  • SimplicialSet_finite at 3113

AbstractSimplex AbstractSimplex represents one simplex where the vertices are numbered sequentially from 1 unless there are degeneracies specified.

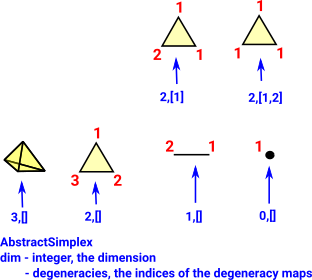SimplicialSet

sage: from sage.topology.simplicial_set import AbstractSimplex, SimplicialSet
            sage: v = AbstractSimplex(0)
            sage: w = AbstractSimplex(0)
            sage: e = AbstractSimplex(1)
            sage: X = SimplicialSet({e: (v, v)})
            sage: Y = SimplicialSet({e: (w, w)})

This is a hierarchy: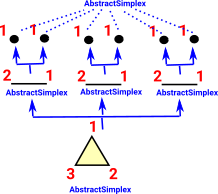

SimplicialSet_arbitrary inherits from Parent which makes them containers.

SimplicialSet_finite

SimplicialSet_finite inherits from SimplicialSet_arbitrary and GenericCellComplex

A simplicial set `X` is a collection of sets `X_n`, the
    *n-simplices*, indexed by the non-negative integers, together with
    face maps `d_i` and degeneracy maps `s_j`.  A simplex is
    *degenerate* if it is in the image of some `s_j`, and a simplicial
    set is *finite* if there are only finitely many non-degenerate
    simplices.

defined by data parameter:

``data`` should have one of the following forms: it could be a
    simplicial complex or `\Delta`-complex, in case it is converted to
    a simplicial set. Alternatively, it could be a dictionary. The
    keys are the nondegenerate simplices of the simplicial set, and
    the value corresponding to a simplex `\sigma` is a tuple listing
    the faces of `\sigma`. The 0-dimensional simplices may be omitted
    from ``data`` if they (or their degeneracies) are faces of other
    simplices; otherwise they must be included with value ``None``.

Dictionary

key	value
nondegenerate simplices of the simplicial set	a simplex `\sigma` is a tuple listing the faces of `\sigma`

Product

One way to do this is find all combinations and then filter out those that are not correctly ordered.

product(A, B) returns the same as ((x,y) for x in A for y in B).

see Python code here.

We can extend this from a product to a pullback with further filtering.

Other Sage Code

• Sage simplicial sets documentation
• Sage simplicial sets code - category - definition of SimplicialSets
• Sage simplicial sets code - homology
• Sage simplicial sets code - topology - examples
• Sage simplicial sets code - topology - morphisms and homsets of simplicial sets

 

EuclideanSpace

home