There are many types of groups:
- Groups with a finite number of objects such as MOD(N).
- Groups with an infinite number of objects such as R(2)
Abelion Groups
In general, for groups, there is no requirement for commutativity, so a * b
is not necessarily equal to b * a. We can consider this as an optional property,
if a group does have a commutativity property it is known as an Abelion Group.
Finite Simple Groups
Simple groups are goups which don't have any normal subroups (apart from the identity and the group itself). This is a similar concept to prime numbers in number theory.
These were clasified by 1980 and consist of:
- Cyclic Groups of Prime Order
- Alternating Groups
- Lie Groups
- Sporadic Groups (26 of them)
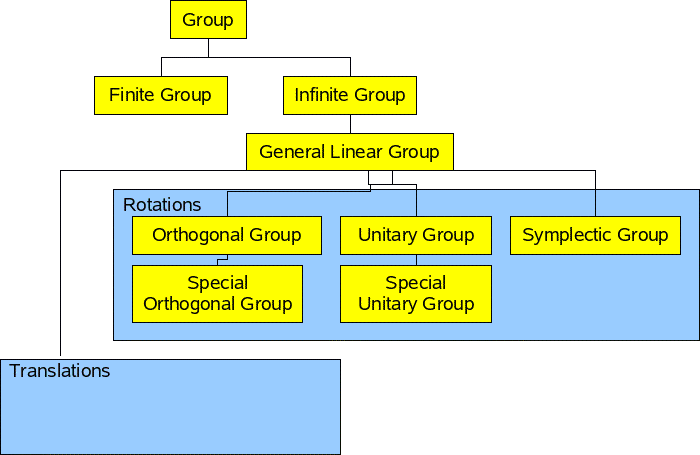
We can define subgroups of groups by specifying constraints. Here are some groups that are relevant to rotations:
Translations are relatively simple, for instance, we could use vectors with the operation of addition. A topic that interests me is the affine transforms as this can represent the movement of solid bodies, translations and rotations. Could anyone help me extend this page to more fully explain affine transforms.
A group can be put together from two subgroups by using the 'semidirect product'. The usual way to represent affine transforms is to use a 4x4 matrix of real numbers.
Finite Groups
See finite groups for more detail.
Dihedral Groups
Dn represents the symmetry of a polygon in a plane with rotation and reflection.
n represents the
- D3 = triangle
- D4 = square
- D5 = pentagon
- …
The group operation is composition.
general form of Cayley table:
| rotation |
reflection |
| reflection |
rotation |
Classification of Lie Groups
The infinite simple lie groups can be classified into the classes shown below. They are called simple, although they don't seem very simple to me, I think this is because it is 'simply connected space'. In topological terms, this means that it is one piece and does not have any holes. In other words, by using every combination of the generators we can generate every possible value.
Lie algebras are direct sums of simple Lie algebras so the classification of Lie algebras reduces to the classification of simple Lie algebras.
A series - The special unitary group, SU(n).
A square matrix is unary if :
UH = U-1
Where:
- UH = the conjugate transpose of U (the conjugate transpose is also known as adjoint matrix, adjugate matrix, hermitian adjoint or hermitian transpose). The conjugate matrix is the complex conjugate of each element.
- U-1 = inverse of U
The group SU(2) is equivalent to (is isomorphic to) the set of unit length quaternions with multiplication. Therefore SU(2) can be used to represent rotations in 3 dimensions (similar to SO(3)).
SU(n) can be represented by n x n matrices with unit determinant, with the operation of multiplication, where each element in the matrix is a complex number.
SU(n) is a subgroup of the unary group U(n) which is a subgroup of the general linear group GL(n).
B series - The special orthogonal group, SO(n).
The special orthogonal group can be used to represent rotations in 'n' dimensions. It has the property that length and shape (Form) is preserved.
The orthogonal group is a subgroup of the 'general linear group' GL(n), therefore this group can be represented by an n x n matrix.
The when represented by matrices the orthogonal group has the useful property that to find its inverse just transpose its rows and columns.
T T* = T* T = 1
where:
- T* = transpose of matrix T
- 1 = identity matrix
Every orthogonal matrix has determinant either 1 or −1. If the O(n) group restricted to determinants of +1 then known as the special orthogonal group SO(n).
C series - The symplectic group, Sp(n).
The symplectic group preserves volume and vector space orientation
The name symplectic group can refer to two different, but closely related, types of mathematical groups. See this article by John Baez.
Can be represented by matrices containing real numbers, complex numbers or quaternions.
symplectic matrices have unit determinant
Symplectic transforms preserve a nondegenerate, skew-symmetric, bilinear form (i.e. B(v,w)= - B(w,v))
D series - Special orthogonal group, SO(n) even dimension.
Note: SO(4) is not a simple group.
This is the orthogonal group with even dimension.
Exceptional algebras
These are the groups G2, F4, E6, E7, E8
They seem to involve matrices whose elements are octonions.