We will first look at differentiation with respect to some dimension outside the complex space (such as time) and we will see that we can treat the real and imaginary parts separately so can use ordinary calculus methods.
We then go on to the more interesting case where we are differentiating with respect to the complex plane.
Complex Number Differentiation with respect to Scalar
To differentiate a complex number with respect to a scalar, say 'x', we individually differentiate each element with respect to 'x'. So if:
f(x) = a + b i
then:
d f(x) / dx = d(a /dx) + d(b /dx) i
So to give a more specific example if:
f(x) = xn + sin(x) i
then:
d f(x) / dx = n*xn-1 + cos(x) i
So this is quite simple, provided that we can differentiate the elements of a complex number, we can differentiate the whole complex number.
Complex Number Differentiation with respect to another Complex Number
Since division of one complex number by another will give a result for non-zero values (unlike vectors) we can define differentiation with respect to another complex number. What are the rules of such differentiation? What applications does it have?
Effect of complex functions on infinitesimal square
When we looked at complex functions on this page we saw that many functions (such as w->x², w->1/x, w->ex) are conformal, that is they preserve angles, this means that infinitesimal squares in the z-plane are mapped to infinitesimal squares in the w-plane. As we can see in the following diagram, on the large scale the squares are distorted, but as we make the squares smaller, they approach square shape:
| z plane | w plane | |
|---|---|---|
 |
--> w=z² |
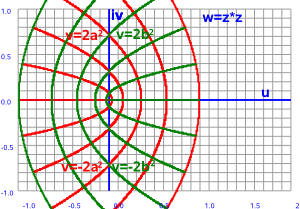 |
These infinitesimal squares may be expanded/contracted and rotated but they remain squares.
This can be analysed by using the Jacobian matrix:
| J= | ∂xu | ∂yu |
| ∂xv | ∂yv |
where:
- J=Jacobian
- ∂xu = ∂u/∂x
- ∂yu = ∂u/∂y
- ∂xv = ∂v/∂x
- ∂yv = ∂v/∂y
If we take: w=z² then u = x² - y² and v=2xy
∂u/∂x = 2x
∂u/∂y = -2y
∂v/∂x = 2y
∂v/∂y = 2x
So in this case the Jacobian is:
| J= | 2x | -2y |
| 2y | 2x |
So the square function multiplies each dimension by 2 (so area on each infinitesimal square is multiplied by 4) leaving the rotation factor:
| x | -y |
| y | x |
we can make it clearer by letting x=r*cos(θ) and y=r*sin(θ) (switching to polar coordinates) which gives:
| r*cos(θ) | -r*sin(θ) |
| r*sin(θ) | r*cos(θ) |
We can see from the plot above that r=1 and θw=θz/2
Conditions for Analytic Function
In order for the function to be differentiable and integratable it must be analytic. This means that infinitesimal shapes must retain their shape, so infinitesimal squares must map to infinitesimal squares although they can be expanded/contracted and rotated. This means that the expansion must be the same in both dimensions. For an intuitive exploration of the implications of this see this page.
Cauchy-Riemann Equations
The requirement that the expansion must be the same in both dimensions gives:
∂u/∂x = ∂v/∂y
∂u/∂y = -∂v/∂x
we can express this in terms of the Jacobian
| J= | a | -b |
| b | a |
where:
- a = ∂u/∂x = ∂v/∂y
- b = ∂v/∂x = -∂u/∂y
Complex Differentiation
So far we have looked at what complex functions do to infinitesimal squares but we have not actually differentiated these functions.
For instance is there an equivalent to:
d f(x)/dx = limitΔx-›0f(x+Δx) / Δx
when x is a complex number?
Complex Number Integration
As with differentiation we can integrate a whole complex number by individually integrating each element. So if:
f(x) = a + b i
then:
![]() f(x) dx = (
f(x) dx = (![]() a dx) + (
a dx) + (![]() b dx) i
b dx) i
