Here we want to calculate the exponent of a quaternion. We will try two approaches:
However, before we start, it will be useful to review some identies.
Useful identities
There is a very useful identity, which is,
e(a+b) = ea * eb
However this only applies when 'a' and 'b' commute, so it applies when a or b is a scalar for instance.
The more general case where 'a' and 'b' don't necessarily commute is given by:
ec = ea * eb
where:
c = a + b + a×b + 1/3(a×(a×b)+b×(b×a)) + ...
where:
- × = vector cross product
This is a series known as the Baker-Campbell-Hausdorff formula.
This shows that if when a and b become close to becoming parallel then a×b approaches zero and c approaches a + b so the rotation algebra approaches vector algebra.
example
lets try a=i and b=j
so
- a×b = i × j = k
- (a×(a×b) = i × k = -j
- b×(b×a) = -j × k = -i
so c = i + j + k - 1/3(j+i) + ...
which gives:
ei * ej = e(i + j + k - 1/3(j+i) + ... )
Other Identities
ln(q^q') = ln(q) * q'
Polar Form
We can express a quaternion as a scalar + bivector:
q = s + b
So can we take the exponent of both sides?
eq = es * eb
Yes, because a scalar commutes with other grades.
The exponent of a scalar is described here.
How do we take the exponent of a bivector?
We can use:
eiθ = cos(θ) + i sin(θ)
but we shouldn't use 'i' because we use 'i' as one of the imaginary dimensions. Instead we will use:
- 'I' representing the rotation plane
- θ representing the rotation angle
eIθ/2 = cos(θ/2) + I sin(θ/2)
Comparison with Complex Numbers
When we looked at complex numbers we saw that they could be represented in what is known as the polar form:
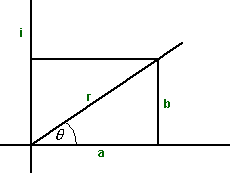
r (cos(θ) + i sin(θ))
in other words replace:
- a = r cos(θ)
- b =r sin(θ)
we can use eiθ = cos(θ) + i sin(θ) to give the exponential form:
r eiθ
To combine the result of two rotations, for example rotate by θ1 then rotate by θ2, then we multiply the corresponding complex numbers because:
ei(θ1+θ2) = eiθ1 * eiθ2
Can we do the same with quaternions to represent rotations in 3D?
If we could it would be very useful! For instance, it would be very useful to use:
e(a i + b j + c k) = ea i * eb j * ec k
Unfortunately that doesn't work
e(a + b) = ea * eb
is valid when 'a' and 'b' are scalar numbers or complex numbers but it does not work when 'a' and 'b' are quaternions or bivectors (the imaginary part of quaternions). This is because bivectors do not commute for multiplication but they do commute for addition, therefore if we swap a and b in the above equation the left hand side will not change but the right hand will, therefore the equation cannot be true for bivectors.
The valid form of this equation for bivectors is:
ec = ea * eb
where:
c = a + b + a×b + 1/3(a×(a×b)+b×(b×a)) + ...
This is a series known as the Baker-Campbell-Hausdorff formula.
This shows that if when a and b become close to becoming parallel then a×b approaches zero and c approaches a + b so the rotation algebra approaches vector algebra.
An example of this might be living on the surface of the earth which, on the small scale, is like being on a flat surface.
Infinite Series
I have not found a version of Euler's equation which applies to quaternions so we need to calculate it ourselves.
The only method that I can think of is to calculate the exponent using the series:
| e(q) = |
|
|
Where:
- q = a + i b + j c + k d
- n= integer
- e = 2.71828
We have to be careful with quaternions because they are not in general commutative. I think the above series applies but I'm not absolutely sure.
We now need to plug in a value for (q)n which we have calculated on this page.
