Prerequisites
On these pages I have used calculus notation, this is very powerful but may be intimidating if you are not used to this notation. dx/dt means the rate of change of x with t , for more information see:
Uniform Velocity
If an object is moving at a constant speed in the x-direction, without rotation, its motion is given by:
v = dx / dt
or integrating:
x = ∫v dt
In the more general case of translation in 3 dimensions, velocity is a 3 dimensional vector:
= 
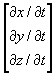= d
/ dt
For further information about differentiation see here
Velocity of solid object
Unusually the velocity of a solid body is taken to be the velocity of the centre of mass (explained in the dynamics section). However, the velocity of a solid object could be taken as the velocity of any point on the mass, for example on say the hand of a robot arm, it may be more convenient to use the part of the hand connected to the wrist.
The velocity of any other point on the object will be the objects velocity + and difference due to the objects rotation. If the object is rotating then each particle, which makes up the object, will have a different instantaneous velocity
Modeling velocity using matrices
if,
a(t)=
[R(t)]l
where:
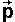- a(t)
= a point represented by a vector in absolute coordinates which is moving (i.e.
is a function of time)
- [R(t)] = a rotation matrix which is a function of time.
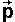- l
= a fixed point represented by a vector in the objects local coordinates.
In other words, if we take a fixed point on an object, and transform the object by multiplying it with a rotation matrix, which is a function of time, then we will get a vector which is rotating as defined by the matrix.
If we want to get the velocity of this vector then we need to differentiate the matrix t give,
a(t)=
[
(t)]l
where:
- a(t)
= the velocity of the point in the first equation
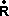- [(t)]
= the matrix from the first equation which has now been differentiated.
Representing Velocity in program
Velocity in 3D space can be held in a 3D vector (see class sfvec3f). For an example of how this might be used in a scenegraph node, see here.
