Assuming the relative motion 'v' is along the x dimension then x -> x0 + vxt
or if we have components of velocity in all dimensions the transform will be:
|
= |
|
|
where:
- vx,vy,vz= relative velocity of the two reference frames in x,y and z directions.
- x,y,z= position in original frame.
- x',y',z'= position in transformed frame.
in other words point:
|
is transformed to: |
|
The nature of this transform is a shear (also known as skew) transform:
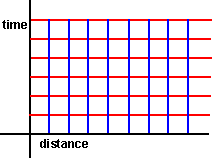 |
—» | 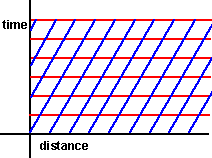 |
When doing this we choose to make time 'absolute' in that the time lines are left horizontal wheras the position lines are skewed althogh I guess that this is just a covention and we could have skewed the time and made the distance absolute.
Shear (skew) Transform Matrix
The shear transform has the following characteristics:
- determinant = 1
- trace = dimension
for example the two dimensional matrix
| a | b |
| c | d |
we have:
a+d=2
ad-bc=1

