There may be multiple ways to represent a given algebraic structure, to take a simple example, the natural numbers. Two possible ways to represent this are:
- As an infinite set with an operation 'plus' which takes two elements of the set and returns another.
- As two functions: n=zero() and succ(n) which return 0 and n+1 respectively.
So they represent the natural numbers like this:
| set + structure | functions |
|---|---|
| 0 | zero() |
| 1 | succ(zero()) |
| 2 | succ(succ(zero())) |
| 3 | succ(succ(succ(zero()))) |
| 4 | succ(succ(succ(succ(zero())))) |
| ... |
The first is a much more practical form of notation but the second is sometimes helpful in understanding the structure. We can view these as complementary ways to approach the same structure.
This applies to many algebraic structures, another example could be finite groups, there are many ways to encode finite groups: (Cayley Table, Cayley Graph, Permutations, Group Presentation, Group Representation). Permutations for groups are like the functional approach to natural numbers above.
This duality can be generalised even more, we will discuss this when we get to category theory and in particular: Yoneda lemma.
For now we will follow the set+structure approach (Universal Algebra), lets look at another algebraic structure: vectors we have various levels of generality:
| Level | Examples for vectors |
|---|---|
| Algebraic theory | Axioms that apply to all vectors such as: A+B=B+A |
| Algebraic variety |
|
| Model |
|
| Element |
|
So at the top level we talk about an 'algebraic theory' or 'equational theory', other examples are 'set theory', 'group theory', 'graph theory' and so on. At this level we can define the axioms that apply in the theory, at a slightly more specific level we can define the theory in terms of:
- a set
- some operations on the set.
Below this we have a model of the theory, that is a concrete vector that is well defined enough for us to create elements and combine them in various ways.
I am not sure this terminology is rigorsly defined, here, or in mathematics generally. There is a good discussion of these issues on this site: John Baez: Finds in Mathematical Physics 200.
Algebraic Structure
So lets look at the set+structure approach a bit more. Here we look at some various types of structure:
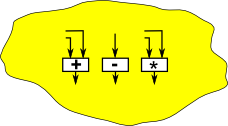
Groups
This consists of:
- A finite or infinite set
- An operation on the set
- An inverse operation
Groups are discussed on these pages.
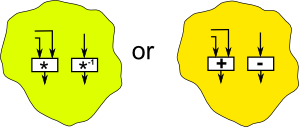
Rings
Rings have two operations (see this page).
Fields and Vector Space over a Field
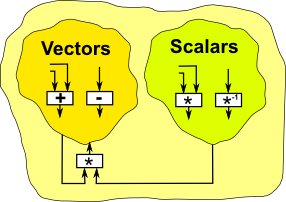
Fields are more specific than rings, they can be scalars when multiplied by vectors.
Specific Algebras
In order to program 3D simulations, games, etc. it is useful to be able to work with different algebras such as,
- Integers,
- Real Numbers,
- Vectors,
- Complex Numbers
- Quaternions,
- Matrices
- Multi Vectors (Clifford Algebra, Geometric Algebra)
Most of these algebras have operations on them such as addition and multiplication. We may be familiar with real number algebra, but when we are working with different algebras different rules may apply, therefore it is useful to explicitly define the rules.
Commutative
An operation is commutative if the order of its operands can be reversed without affecting the result. This is usually expressed in terms of arbitrary elements of the algebra (here denoted x and y).
| ( |
x * y = y * x |
This says that for all values of x and y then x * y is always equal to y * x. Below we will see that there are ways to express this without having to use arbitrary variables.
Addition is commutative but multiplication may, or may not be, commutative. See table below. For example matricies and quaternions don't have commutative multiplication.
Associative
An operation is associative if the order of doing multiple operations is not important. For example:
| ( |
x * (y * z) = (x * y) * z |
Distributive
When there are two operations in this algebra say, + and *, then * is said to be distributive over + if:
| ( |
x * (y + z) = (x * y) + (x * z) |
Other Ways To Represent These Properties
So far we have described these algebraic axioms in terms of arbitrary variables named x,y and z. This is the easiest way to intuitivly understand the axioms, however when working with computers it may be better if we can find an altenative notation which eleminates these arbitrary variables, also this may help us to generalise to any structure which has a given system of axioms (see algebraic variety), that is we want to seperate the structure from the objects the structure works on.
To do this we need to abstract (lift) up a level and describe these properties in terms of its external properties. There are two mathematical subject areas on this site which take this approach:
- Category Theory - see functors and here.
- Combinatory Logic
Commutative Law
For instance in combinatory logic the commutative law, which we defined above:
| ( |
x + y = y + x |
We change + as a prefix rather than an infix operator:
| ( |
+(x,y) = +(y,x) | |
| +(x,y) = (C+)(x,y) |
Where C means: swap functions as explained on the combinatory logic page.
So we can cancel out the elements (x,y) and just represent the commutative axiom as:
+ = C(+)
So using operators we don't have to describe axioms in terms of arbitrary elements.
Associative Law
We can also 'lift' the associative law, on the category theory pages the associative law, which we defined above:
| ( |
x * (y * z) = (x * y) * z |
On this page we changed * which acts as an infix operator to μ which acts as a prefix function and so we get:
| μ(x,μ(y,z)) = μ(μ(x,y),z) | prefix version of above |
| μ(id×μ)(x,y,z) = μ(μ×id)(x,y,z) | rearrage to make function of (x,y,z) |
| μ•(id×μ) = μ•(μ×id) | 'lift' that is cancel out (x,y,z) |
Algebras
| * distributive over + | Multiplication commutative | Multiplication associative | |
| Real Numbers | yes | yes | yes |
| Complex Numbers | yes | yes | yes |
| Quaternions | yes | no | yes |
| Octonions | yes | no | no |
| Vectors | yes | no | no |
| Matricies | yes | no | yes |
| Multi Vectors | yes | no | no |
For further information see group theory.
Other Algebra Concepts to be Covered
- Sets
- Numbers - infinite sets, ordered sets
- Functions (mappings) - between elements, between groups or rings
- Binary operations
How do I design an Algebra?
These different algebras listed above all use the same addition and multiplication operations, the difference seems to be the number of dimensions and the way that these dimensions interact.
In all the above cases addition just adds the terms from corresponding dimensions.
Multiplication combines numbers across dimensions, if it did not then we might as well treat each dimension independently. So it is multiplication which differs between each of the above algebras and gives each its own 'flavor'.
In fact, in many cases when applying these algebras in practical cases, we may use only the multiplication operation (see group theory) for example, quaternions when applied to 3D rotations.
So it seems to me that we can define these algebras by a table showing how the multiplication operator combines each dimension with each other dimension.
Some of the key factors seem to be:
- Number of dimensions.
- Result of squaring a dimension (+1 or -1)
- Does the operation conserve distance (this seems very geometry oriented for pure algebra?)
From what I can tell the commutative and associative laws for multiplication would be determined from the table
