On this page I would like to think about whether there is any way to get the powerful mathematical capabilities of SPAD but with improved programming environment such as IDE, useful error messages, access to the java/scalar library that come with a language such as Scala.
We have already seen, on this page, that SPAD has elements of both object oriented and functional styles of programming, strong typing and so on. I would therefore like to compare SPAD to Scala which also has these things. In fact when comparing SPAD and Scala the code looks remarkably similar, so what would it take to modify Scala to be able to model mathematics as well as SPAD? (not necessarily the exact same syntax).
There is a general correspondence (although important details differ greatly) between the top level constructs of the language.
| SPAD | Scala | Java |
|---|---|---|
| category | trait | interface |
| package | singleton object | class with static functions |
| domain | class | class |
There are many differences but as a start the following seem quite fundamental issues:
- Generics differences.
- Matching and coercions.
Generics Differences
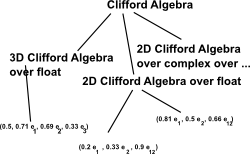 |
When we try to model a concept like 'Clifford algebra' we might end up with 3 levels of abstraction:
|
In SPAD a CliffordAlgebra is implemented as a 'domain', the types of Clifford algebra are given by parameters to the domain definition (note: these are not parameters of a runtime instance).
CliffordAlgebra(n, K, bLin): T == Impl where
n: PositiveInteger
K: Field
bLin: SquareMatrix(n, K) |
So how could we do this in Scala? Well the parameter K: Field is the easiest because it is a type and type parameters can be handled by generics (type parameterization)
class CliffordAlgebra[K] |
There are still issues because we want to constrain K to be a Field but at least there seems to be a mechanism for doing roughly what we want.
How do we deal with 'n' and 'bLin' ? These are not types but we want them to determine subtypes.
Of course we could make 'n' and 'bLin' parameters in the CliffordAlgebra constructor but that would mean that they would have to be specified every time an instance were created and stored in every instance which would be very wasteful.
The best solution I can think of is to implement this two layer abstraction by two levels of objects:
- CliffordAlgebraType[K]
- CliffordAlgebra[K]
An instance of CliffordAlgebraType could be created for each combination of (n, bLin) that we want to use and a reference to this type could be a single parameter which we pass to the constructor every time we construct an instance of CliffordAlgebra[K].
This is quite messy and it means that we potentially have to create two classes when we want to create a new algebra. This is not nearly as efficient or powerful as SPAD where it can all be done easily in one 'domain' definition.
Matching and Coercions
This is one of the most powerful (and sometimes one of the most dangerous) features of SPAD. It seems to be related to a lot of cases of unexpected behavior that seem to come up on the FriCAS forum.
Imagine that we have some expression in SPAD like:
s * v
Then the operation '*' might be defined in many places, so matching is used to determine which definition is most appropriate for this individual case.
So for instance if 's' happens to be a floating point number and 'v' happens to be a vector then the matching looks for a declaration of the form:
*(s: Float, v: Vector Float) -> Vector Float
and then applies the function associated with that.
Note that:
- We need to match, not generic Vectors but Vectors over Floating point numbers.
- The matching may also involve matching the output type, which could get complicated where operations are nested.
- This type of matching is done to find the most appropriate implementation for Unary and Binary operations as well as general functions (only the binary operation is illustrated here).
- If operations are marked as commutative then we want to be able to reverse the operands.
- Matching may also involve Coercing to related types (boxing).
To explain this last point imagine that we want to multiply an integer by a vector, we don't have an explicit Integer * Vector defined but we do have a method to convert an Integer to a Float so we can use the above declaration. This needs to work, not only with built in types like Integer and Float but with coercions between user defined types.
So how could we do this in Scala? The object oriented way of doing this does not seem very natural in the mathematical world, so rather than this:
v = new Vector(0.2f,0.3f)
s = 0.5f
result = v.mult(s)
it would be more natural to do this:
result = 0.5f * vector(0.2f,0.3f)
In Scalar this is equivalent to:
result = (0.5f).*(vector(0.2f,0.3f))
That is '*' is called on float with vector as a parameter, even if we get this working we would have to define float times vector in one class and vector times float in a different class which is very messy.
Perhaps there could be some compromise like:
result = 0.5f (Vector.*) vector(0.2f,0.3f)
In other words we explicitly tell the program which class holds the most appropriate multiply operation.
But if we want scala to work like SPAD then it needs to match against all possible operations and functions rather than specifying explicitly.
Scalar seems to have very powerful pattern matching, for example 'case classes' but from what I can see the programmer has to call an explicit 'match' command on external data, is there some way that this match could be done whenever any * is called internally within the program? In fact it would have to be for every unary or binary operation and every function call!
The other powerful pattern matching built in to scala seems to be 'combinator parsing' and I get the impression that this can be applied to the internal workings of scala? (by using a Compiler Plugin) However I don't understand it or know if it would help in this application?