Here we look at structure preserving (sometimes called monotone) morphisms between ordered sets.
In the case of morphisms between ordered sets we want to check the arrows are preserved: f(a≤b ) = f(a) ≤ f(b) |
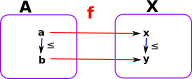 |
Endomaps
How many structure preserving maps of a lattice back to itself?
In some cases, we want to map the structure to the whole of itself so, the top and bottom elements map to themselves. If there are different branches in the ordering we may be free to permute them. |
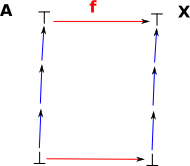 |
| In some cases we want to make a copy of the structure inside itself, even though some nodes will be merged together. This allows us to model recursion and it allows some fixpoint theories to emerge. | 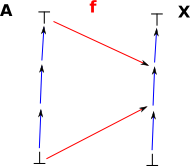 |
Order Embedding (Order Isomorphism)
An order embedding makes a copy of the structure inside itself, as above, but it does not merge nodes. That is, it makes a faithful copy. Therefore the mapping is one-to-one, an isomorphism.
Order Similarity
The posets P and Q are order similar if there is an isomorphism from P to Q.
An order similarity is an equivilance relation (transitive,symmetry,reflexive).
Every poset is order-isomorphic to an inclusion poset.
