Maths - Morphism Examples

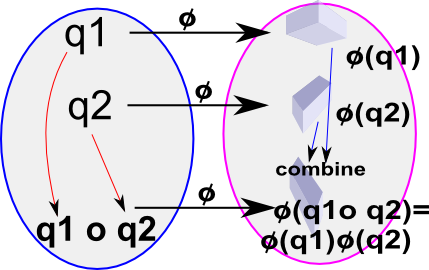
Here we look at some examples to see if they are morphisms, that is, does:

φ(v1) o φ(v2) = φ(v1 o v2)

where:

• φ = isomorphism mapping
• v1 and v2 = elements of group
• o = group operation

Example 1 vector addition with mapping = shift of origin

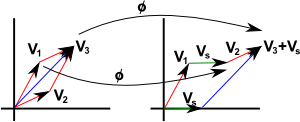
With mapping φ between vector additions of fixed offset V_s so each vector is transformed by:

φ(V) = V + V_s

This is not an isomorphism since:

(V₁ + V_s) + (V₂ + V_s) ≠ (V₁ + V₂) + V_s

however:

(V₁ + V_s) + (V₂) = (V₁ + V₂) + V_s

so if we treat V₂ as an offset and don't transform it then the equation matches.

Example 2 vector addition with mapping = scaling

With mapping φ between vector spaces of scalar multiplication by M so each vector is transformed by:

φ(V) = M*V

This is an isomorphism since:

V₁*M + V₂*M = (V₁ + V₂) *M

Example 3 multiplication with mapping = scaling

With mapping φ between vector additions of fixed scalar multiplication by M so each vector is transformed by:

φ(V) = M*V

This is not an isomorphism since:

V₁*M * V₂*M ≠ (V₁ * V₂) *M

So what mapping φ can we use with multipication to form an isomrphism? A common form is the 'sandwich product':

φ(v) = q v q^-1

I have used q here to indicate a quaternion because the various types of vector product don't really have the correct properties. Use of the sandwich product in this way is discussed on this page.

so

φ(q1*q2) = q q1 q2 q-1 = q q1 q-1 q q2 q-1 = φ(q1)*φ(q2)

(since q-1 q =1)

So we can see that this sandwich product (conjugacy) has the right properties for an isomorphism

EuclideanSpace

home

Group Theory

Rules of Mathematical Operations

Rotating a Cube