It is quite difficult to give a physical meaning to a quaternion, it is just a quantity which represents a rotation. If you need a physical meaning then this is probably the best way to think of it:
q = cos(a/2) + i ( x * sin(a/2)) + j (y * sin(a/2)) + k ( z * sin(a/2))
where:
- a=angle of rotation.
- x,y,z = vector representing axis of rotation.
So it is closely related to the axis angle representation of rotations.
In the following diagram:
- Rotation Axis: is a line we are rotating around, that is, during the rotation points maintain the same distance from the rotation axis.
- Rotation Plane: During the rotation points in the plain remain in the plane and other points remain the same distance from the plane.
Note: we are talking about rotations about the origin so both the rotation axis and the rotation plane go through the origin.
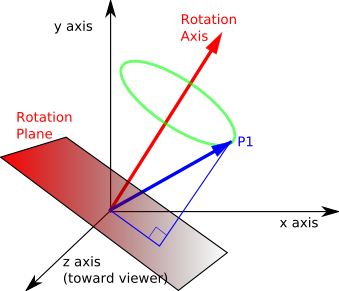
Imagine a point P1 which is a unit distance from the origin, we will be rotating it through an angle (a) to P3 through midpoint P2.
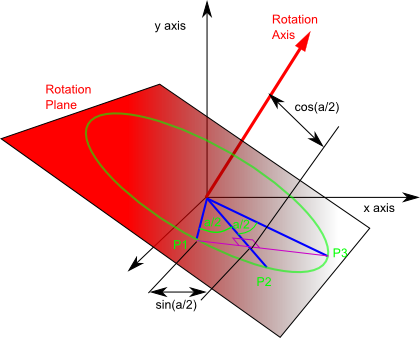
So the point P1 is transformed to P3, if it travels in a straight line it passes through a point cos(a/2) from the rotation axis and sin(a/2) from both P1 and P3.