A finite state machine or automation provides a simple model of computation, a way to reduce the complexities of a computer to its essence, in addition to its theoretical significance this can be a good way to tackle certain types of practical problem.

The current state is determined by past states of the system and the inputs to the system (it has a memory). A transition indicates a state change and is described by a condition that would need to be fulfilled to enable the transition. An action is a description of an activity that is to be performed at a given moment.
State diagram
We could describe the machine in terms of transitions, for each combination of state and input this will determine the transition function which gives the next state:
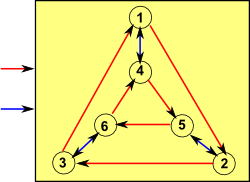
State transition table
| Condition↓Current state -> | State 1 | State 2 | State 3 | State 4 | State 5 | State 6 |
|---|---|---|---|---|---|---|
| Input red | State 2 | State 3 | State 1 | State 5 | State 6 | State 4 |
| Input blue | State 4 | State 5 | State 6 | State 1 | State 2 | State 3 |
Outputs
There are different variants, for instance,
- Moore machine - machines having actions (outputs) associated with states.
- Mealy machine - machines having actions (outputs) associated with transitions.
Mathematical Model
In its essence the model consists of (Σ,S,s0,δ), where:
- Σ is the input alphabet (a finite, non-empty set of symbols).
- S is a finite, non-empty set of states.
- s0 is an initial state, an element of S.
- δ is the state-transition function: δ: S × Σ -> S (in a nondeterministic finite state machine it would be δ: S × Σ -> (S1,S2,S3,S4) i.e., δ would return a set of states).
In some circumstances (for instance Mealy machine) we may need to add:
- F - the set of final states (subset of S) states, if any that result in the machine stopping.
- Γ - the output alphabet (a finite, non-empty set of symbols).
- ω - the output function - a mapping from the states to output.
