Here we look at a two dimensional euclidean space embedded in a three dimensional projective space, we are using the stereographic model to do this projection. For a more general discussion of stereographic projection see page here.
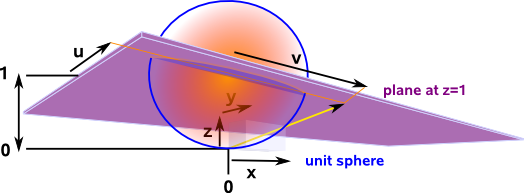
In two dimensional projective space using stereographic model:
- Straight lines in euclidean space map to great circles (or semi circles) in projective space.
- Horizontal lines meet at (0,0,0) which is the point at infinity for horizontal lines.
- Vertical lines meet at (0,0,0) which is the point at infinity for vertical lines.
- infinity, in any direction, is represented by the same point (0,0,0).
From the above we can see that, as we move away from the origin, lines that cross at 90° in euclidean space do not cross at 90° in projective space. So angles away from the origin are not conserved by the projection.
Derivation for translation between projective (stereographic) and euclidean spaces
As for the hemisphere model, since we are projecting using a straight line, there is a linear relationship between a point on the plane and its projection on the sphere:
|
= λ |
|
where:
- (x,y,z) = projective coordinates
- (u,v) = euclidean coordinates
- λ = expansion factor of vector: function of (x,y,z) or (u,v)
Dividing the top two rows by the bottom row gives the euclidean coodinates in terms of the projective coordinates:
|
= |
|
To go the other way from the projective coordinates to the euclidean coodinates we need to use the information that the coordinates are constrained to a unit sphere centred at (0,0,1) so:
x² + y² + (z-1)² = 1
rearanging gives:
x²/z² + y²/z² + (z²-2z +1)/z² = 1/z²
u² + v² + 1 = 2z/z² = 2/z = 2/λ
λ = 2/(u² + v² + 1)
substituting this into the first vector equation gives:
|
= 2/(u² + v² + 1) |
|
Alternative Coordinate System
So far I have chosen the origin of the x,y,z coordinate system as the projection point as this seems the simplest way to do it. However other sources (see Doran & Lasenby - Geometric Algebra for Physisits book on right of this page and also the Wikipedia page on stereographic projection) seem to use a coordinate system where the origin of the x,y,z coordinate system is at the centre of the sphere. So in order to relate to these other sources I will repeat the above with this coordinate system:
We will now have:
|
= λ |
|
So
|
= |
|
since the origin is on the plane being projected and
x² + y² + z² = 1
dividing both sides by (z-1)² gives:
x²/(z-1)² + y²/(z-1)² + (z²-1)/(z-1)² = 0
u² + v² + (z +1)/(z-1) = 0
u² + v² + (λ+2)/λ= 0
u² + v² + 1 +2/λ= 0
λ= -2/(u² + v² + 1)
substituting this into the first vector equation gives:
|
= -2/(u² + v² + 1) |
|
adding 1 to both sides of row 3 gives:
|
= -2/(u² + v² + 1) |
|
which is:
|
= 1/(u² + v² + 1) |
|

