This page looks at a one dimensional case of stereographic projection for a more general discussion of stereographic projection see page here.
| Here we look at a one dimensional euclidean space embedded in a two dimensional projective space, we are using the stereographic model to do this projection. |
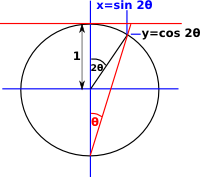 |
In one dimensional projective space using stereographic model:
- A straight lines is mapped to a circle in projective space.
- The point at infinity is given by θ=180 degrees.
Derivation for translation between projective (stereographic) and euclidean spaces
| The line is (1): |
y' = 1 |
| The circle is (2): |
x²+(y-½)²=(½)² |
| from (2): |
x² = (1-(2y-1)²)/4
= (1-4y² +4y -1)/4
= -y² +y |
combining gives:

