Here we look at a one dimensional euclidean space embedded in a two dimensional projective space, we are using the hemisphere model to do this projection.
To represent 'n' dimensions we use 'n+1' dimensions in projective space. So lets start with a one dimensional case which will be represented as a two dimensional projective space. This one dimensional case may not have much practical application but it should allow us to establish the principles as simply as possible.
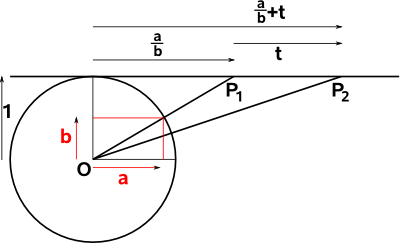
In the diagram above the horizontal line represents the one dimensional space. Points on the line, for example P1 and P2, are represented by the intersection of the horizontal line with a line from the origin O.
So, for instance, the point P1 can be represented by the line from 'O' the origin (the one dimensional space is offset from the origin by one unit).
This line can be represented by its normalised coordinates (a;b), that is the coordinates on the unit circle, although any scale factor 's' which gives (a*s;b*s) does not change the point as it still lies along the O to P1 line. So we can represent P1 by the ratio a/b.
One Dimensional transforms
In one dimension we don't have rotations so lets investigate translations. In the diagram above we want to translate P1 by 't' to P2. Of course we can do this by adding 't' as shown on the diagram but can we apply a transform using a multiplication? This would be useful when we move to higher dimensions and we want to combine translations and rotations.
We know that we can combine rotations using multiplication as described here so can we rotate the O to P line to perform a translation? As we can see from the above diagram this would not be linear because points nearer to 'O' would move more than points further away. Is it possible to use a different type of rotation such as hyperbolic rotation to perform our translation?
|
= |
|
|
Although this approximates projective transforms at small angles it does not work because projective geometry is represented by a shear transform, in order to represent translation by a rotation we need to use a conformal geometry.
Projecting onto a Line
Projecting a plane onto a line is discussed on this page.
To project points on the projective plane onto the line we can use the linear transform:
|
= |
|
|
where:
x'/y' = (m00 x/y + m01)/(m10 x/y + m11)
Algebra of One Dimensional Projective Space
We will start by using matrix algebra and then we will investigate using geometric algebra.
So in matrix and vector we can represent a point in projective space along the line we are using (which is offset by 1) as:
| p |
| 1 |
The transform is represented by this matrix:
| 1 | t |
| 0 | 1 |
This is a shear (also known as skew) matrix.
Multiplying them together gives the offset as required.
|
= |
|
|
Note that in projective space points (meaning location) and translations are represented by different types (unlike vector algebra) this is reasonable as they are different entities.
So we now have a way to perform a translation using multiplication, but at a cost, we are using a shear transform which is non-linear unlike say a rotation.
Combining Translations
If we want to combine two translations t1 and t2 then we can multiply their matricies together to give the required result:
|
= |
|
|
Homogeneous Coordinates in One Dimension
In the above notation we don't yet have the ability to represent points at infinity, so instead of representing the location by 'p' we will instead represent it by a/b in matrix notation our location is represented by:
| a |
| b |
So, for instance, zero will be:
| 0 |
| 1 |
and infinity will be:
| 1 |
| 0 |
The transform is now represented by this matrix:
| 1 | t/b |
| 0 | 1 |
Multiplying them together gives the offset as required:
|
= |
|
|
So the transform depends on the how the location (a;b) is scaled or normalised? Also combining transforms appears to be more complicated if they are normalised differently.
Shear Transform
Shear (also known as skew) transforms can be represented as a linear transforms, that is we can apply the transform by using a multiplication. However it is easier to represent shear transforms using matrices than Geometric Algebra. In order to use Geometric Algebra we may have to revert to using addition but Geometric Algebra has other advantages such as computing 'meet' and 'join'.
The determinant of shear transforms is 1, for instance,
det |
|
=1 |

