Amy de Buitléir has kindly sent me this nice step-by-step example.
It illustrates how it is easier to just work with dual quaternions and forget about vectors..
Ex: We have a prop inside a container, which is inside a scene.
The prop is at (0, 0, 100), specified in the container's co-ordinate system.
The container is at (0, 0, 0), specified in the scene's co-ordinate system.
The container is also rotated +30° around the y-axis.
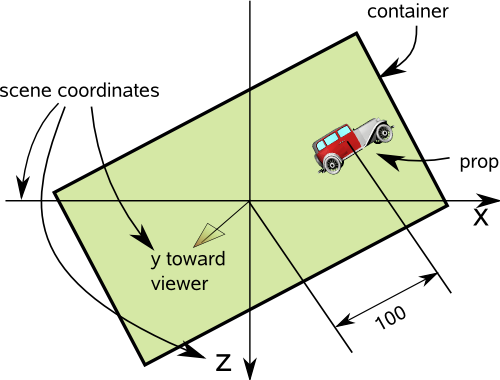
Note: I have shown the coordinates differently from usual (z down, y toward viewer).
Q: What is the location of the prop, specified in the scene's co-ordinate
system?
First, we need to build a dual quaternion to represent the state (location and rotation) of the prop wrt (with respect to) the container. We'll call this dual quaternion Q(prop,container).
The position of the prop with respect to the container can be represented by
the quaternion:
t(prop,container) = (0, 0, 0, 100)
The real part of the dual quaternion Q(prop,container) is 1 because prop isn't rotated. The dual part is:
dual part = (1/2)(real)t = (1/2)(1)(0, 0, 0, 100) = (0, 0, 0, 50)
Q(prop,container) = 1 + ε(0, 0, 0, 50)
Next, we need to build a dual quaternion to represent the state of the container wrt the scene.
t(container,home) = 0 because the container is not translated.
The container is rotated 30 around the y-axis, so
sx2 = sz2 = 0 sy2 = sin(30/2) = 0.2588
cx2 = cz2 = 1 cy2 = cos(30/2) = 0.9659
real part = (0.9659, 0, 0.2588, 0)
dual part = (1/2)(real)t = 0
Q(container,home) = (0.9659, 0, 0.2588, 0) + ε0 = (0.9659, 0, 0.2588, 0)
Now we're ready to calculate the state of the prop wrt the scene:
Q(prop,home) = Q(prop,container) * Q(container,home)
= [1 + ε(0, 0, 0, 50)] (0.9659, 0, 0.2588, 0)
= (0.9659, 0, 0.2588, 0) + ε(0, 0, 0, 50)(0.9659, 0, 0.2588, 0)
= (0.9659, 0, 0.2588, 0) + ε(0, -12.94, 0, 48.295)
We can easily extract the translation from this dual quaternion.
t(prop,home) = 2*real†*dual
= 2(0.9659, 0, 0.2588, 0)†(0, -12.94, 0, 48.295)
= 2(0.9659, 0, -0.2588, 0)(0, -12.94, 0, 48.295)
= 2(0, -25.0, 0, 43.3)
= (0, -50, 0, 86.6)

