Computation Theory

Here we look at theoretical models of computing, such as the following approaches to defining a computer:

Computing is often defined in terms of physical quantities such as 'information' and 'entropy' but here we are discussing computing in mathematical terms [see 11]. In the 1930s, Kurt Gödel, Alonzo Church, Emil Post, and Alan Turing independently gave formal notions of computation in terms of specific mathematical structures.

Computer

A simple model, which resembles the way that computers work, is of a memory whose state is read and modified by a processor. A function, like this, which operates on its own input is called an endofunction. This cycle is continuously being repeated, the element of the endofunction being determined by the program of the processor. 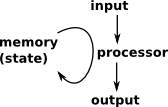computer

Data Types

When we use higher level languages then we start to think of the memory, less of containing a passive state, and more in terms of active entities that have their own operations. This can happen at many levels so structures are embedded in structures and so on.

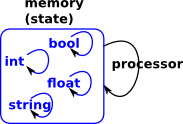higher level computation

Relationship to Algebras

The mathematical concept of an algebra is related to an endofunction as above (see this page). An algebra has 2 extremes the 'initial' algebra and the 'final' algebra. Data types are an initial algebra.

Types

The concept of 'types' arises in both mathematics and computer theory. There are different aproaches we cam take when modelling algebras in computer programs.

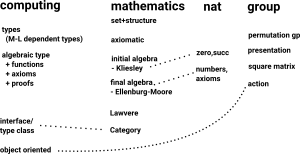
computing maths

Related Structures

If we want to cover the full range of mathematical structures related to computing then we should really include Finite State Machines and Automata. These are coalgebra-like structures which are related to the algebra structures already included.

I was thinking about how to convert a finite state machine into a instance of Lambda, then I realised this is just about implementing stateful code in a pure functional language and Haskell has already solved that problem - use monads (from my limited knowledge of Haskell I get the impression, whatever the problem, the answer is to use monads).

Perhaps FriCAS should have a lattice structure which could then be extended into intuitionistic logic domain. I don't think partially ordered set (setorder.spad.pamphlet) would be in the right form to extend logic domains.

Also graph structures, for instance:

Many of the domains in this document are also tree structures.

Category Theory

Lambek and Scott 1988 [10] show that typed lambda-calculi and cartesian closed categories are essentially the same and intuitionistic logic is closely related to topos theory.

Also the discussion of monads above tends to indicate that they need to be used here.

All of this suggests to me that all the code in this document would benefit from being put into a wider framework based on category theory.

Intuitionistic Logic

The intuitionisticLogic domain implements a Heyting algebra implied by intuitionistic logic similar to boolean algebra.

Intuitionistic or constructive logic is similar to classical logic but where the law of excluded middle is not used.

The implementation starts with a 'free logic algebra' that is an algebra where each combination of inputs to /\ , \/ and ¬ generates a new element. So an expression like T /\ T is just T /\ T and does not simplify.

Then by adding "simplification rules" (should I have called them relators?) then other logic algebras can be implemented (intuitional, ternary, many-valued, boolean) just by adding the "rules".

These "rules" are hardcoded into the /\ , \/ and ¬ implementations (rather than implementing a true rule based system).

Simplification rules :

where:

An option to generalise this code might be to implement the 'free logic algebra' as a category, then intuitional, ternary, many-valued, boolean could be domains which overload /\ , \/ and ¬ with their own sets of rules.

Note: Please be aware that changes may be made in the future to improve and correct intuitionistic logic domain, such as:

Intuitionistic Logic Tutorial

Intuitionistic logic has many possible values: true 'T', false '_|_' and infinitely many other values generated by constructs such as inverse. These can be constructed as follows: 

(1) -> logicF()
(1)  "_|_"
                    Type: ILogic
(2) -> logicT()
(2)  "T"
                    Type: ILogic
(3) -> ~logicT()
(3)  "_|_"
                    Type: ILogic

This logic has different rules from boolean algebra and all constructions do not reduce to true or false. To test out our constructs we will use the following list: 

(4) -> l:List ILogic := [logicF(),logicT(),proposition("a"),~proposition("a"),proposition("b"),~proposition("b")]
LISP output:
((0 F) (0 T) (1 a) (3 NOT 1 a) (1 b) (3 NOT 1 b))
                    Type: List(ILogic)

First we will try 'not': 

(5) -> [(~j)::OutputForm for j in l]
(5)  ["~(_|_)","_|_","~(a)","~(~(a))","~(b)","~(~(b))"]
                    Type: List(OutputForm)

We can print a truth table for 'and' and 'or'. This is the same as boolean logic for true/false values and extended for the unproven case. 

(6) -> matrix[ [(k /\ j)::OutputForm for j in l] for k in l]
(6)
SUB
matrix
["_|_","_|_","_|_","_|_","_|_","_|_"]
["_|_","T","a","~(a)","b","~(b)"]
["_|_","a","a","_|_","(a/\b)","(a/\~(b))"]
["_|_","~(a)","_|_","~(a)","(~(a)/\b)","(~(a)/\~(b))"]
["_|_","b","(b/\a)","(b/\~(a))","b","_|_"]
["_|_","~(b)","(~(b)/\a)","(~(b)/\~(a))","_|_","~(b)"]
                    Type: Symbol

Note: Its hard to read this table in text, it displays better as html on this page

(7) -> matrix[ [(k \/ j)::OutputForm for j in l] for k in l]
(7)
SUB
matrix
["_|_","T","a","~(a)","b","~(b)"]
["T","T","T","T","T","T"]
["a","T","a","(a\/~(a))","(a\/b)","(a\/~(b))"]
["~(a)","T","(~(a)\/a)","~(a)","(~(a)\/b)","(~(a)\/~(b))"]
["b","T","(b\/a)","(b\/~(a))","b","(b\/~(b))"]
["~(b)","T","(~(b)\/a)","(~(b)\/~(a))","(~(b)\/b)","~(b)"]
                    Type: Symbol

'implies' produces the following truth table. 

(8) -> matrix[ [implies(k,j)::OutputForm for j in l] for k in l]
(8)
SUB
matrix
["T","T","(_|_->a)","(_|_->~(a))","(_|_->b)","(_|_->~(b))"]
["_|_","T","(T->a)","(T->~(a))","(T->b)","(T->~(b))"]
["(a->_|_)","(a->T)","(a->a)","(a->~(a))","(a->b)","(a->~(b))"]
["(~(a)->_|_)", "(~(a)->T)", "(~(a)->a)", "(~(a)->~(a))", "(~(a)->b)",
"(~(a)->~(b))"]
["(b->_|_)","(b->T)","(b->a)","(b->~(a))","(b->b)","(b->~(b))"]
["(~(b)->_|_)", "(~(b)->T)", "(~(b)->a)", "(~(b)->~(a))", "(~(b)->b)",
"(~(b)->~(b))"]
                    Type: Symbol

Now that we can do intuitionistic logic with constant values we can go on to represent theories. We can enter a symbolic value as follows: 

(9) -> proposition("p1")
(9)  "p1"
                    Type: ILogic

When applying a symbolic value, then it may not possible to compress as a single node, so the result remains as a tree. So (13) can be reduced to a single value '_|_', because the result does not depend on \verb'a', however in (12) we cannot reduce to a single value. 

(10) -> proposition("a") /\ proposition("b")
(10)  "(a/\b)"
                    Type: ILogic
(11) -> implies(proposition("a"),proposition("b"))
(11)  "(a->b)"
                    Type: ILogic
(12) -> proposition("a") /\ logicT()
(12)  "a"
                    Type: ILogic
(13) -> proposition("a") /\ logicF()
(13)  "_|_"
                    Type: ILogic

applying modus ponens

modus ponens tells us that given: 'a' and 'a->b' then we can imply 'b'. So we first assert 'a' and 'a->b' as follows: 

(14) -> givens := proposition("a") /\ implies(proposition("a"),proposition("b"))
(14)  "(a/\(a->b))"
                    Type: ILogic

We then factor into separate terms: 

(15) -> fgivens := factor(givens)
LISP output:
((1 a) (2 . UNPRINTABLE))
                    Type: List(ILogic)

note: List ILOGIC to OutputForm is fixed in latest FriCAS so it will now display: [a,a->b]

We now apply the deductions function to this list. 

(16) -> deduct := deductions(fgivens)
LISP output:
((1 b))
                    Type: List(ILogic)

so we get the required deduction 'b'

domain ILOGIC ILogic

Variables

Before we get on to the main domains we have some code to represent variables in Lambda and Ski domains. Since we are working in terms of functions then a variable will be a function (possibly a constant function).

There is a category to represent these function variables and there are two implementations of this category so far:

Variables Tutorial

The two implementations: Untyped and Typed which can be constructed as follows: 

(1) -> var("x")$Untyped
(1)  "x"
                    Type: Untyped
(2) -> var("x",proposition("a"))$Typed
(2)  "x:a"
                    Type: Typed
(3) -> parseVar("x:(a->b)")$Typed
(3)  "x:(a->b)"
                    Type: Typed
(4) -> parseVar("x:(a/\b)")$Typed
(4)  "x:(a/\b)"
                    Type: Typed
(5) -> parseVar("x:(a\/b)")$Typed
(5)  "x:(a\/b)"
                    Type: Typed

(1) shows an untyped variable.

(2) shows a typed variable with a simple type "a"

In (3 to 5) we are entering a variable with a more complicated compound types so it is easier to use parseVar to construct from a string although this could have been built from raw types.

Note that the \verb':' binds more tightly than \verb'->' so we need to put brackets around \verb'a->b' so that its read as a type.

There are 3 ways to build up compound types:

We can nest these compound types to build up more complex types.

Variables are not usually constructed directly by the user but instead are used by lambda and ski domains.

Types

There are various ways to interpret the concept of 'type' in the study of both computation and in pure mathematical terms, for example:

We need to be able to model type theory and to do this in a flexable way we must build our own type domains rather than use the types used by SPAD (although a possible future enhancement would be to support SPAD types as a special case but not the general concept of type).

I am trying to develop an abstract model of general mathematical structures here, not a sub-language within FriCAS, so I don't want to over specify this. However I think it would be good to specify a model which is as general as possible and can be expanded to model these things.

So we need various levels of support for types depending on the situation:

Initially, not all of these options are supported by this framework and there are other issues, still to be resolved:

One of the most important flavors to support is simply typed with function types. This is because:

simply typed with type operator for function types

and cartesian products. We can write formation rules for well typed terms (WTT) using the following notation:

Using this terminology the rules are:

Now we will implement variables:

First a common category for the various variable types:

category VARCAT VarCat

Next an implementation of the above category which is intended to work with untyped variables:

domain UNTYPED Untyped

Next an implementation of the VarCat category which is intended to work with typed variables:

domain TYPED Typed

lambda-Calculus

for more details see this page:

Notation

Externally a fairly standard notation is used, as may be familiar to someone using a textbook to study lambda-calculus, or as close as we can get without using unicode. I have used the \verb'\' symbol to stand for lambda. At some stage in the future it may be possible to use unicode lambda symbol but not yet due to compatibility issues.

Internally the domain stores bound variables using De Bruijn index, in most cases this should not concern the user as I/O uses string names for variables. Converting bound variables internally to index values means that the same variable name can be used, in different lambda terms, without ambiguity and without the need for alpha-substitution.

De Bruijn index which is a integer where 

0=inside current (inner) lambda term
1= next outer lambda term
2= next outer and so on
...

We will see how this works in the tutorial below.

So internally the lambda-calculus is stored as a binary tree structure using the following syntax: 

<term> ::= "\" var "."<term> | n | <term><term> | "("<term>")"
where:
\ = lambda
n = De Bruijn index which is a integer where,
0=inside inner lambda term,
1= next outer lambda term,
2= next outer and so on.
var = a string representation of variable (this form is used for
unbound variables)
brackets can be used around whole terms.

Tutorial

On this page we will be working with 'untyped' variables so we create an instance called UNTYP to simplify notation: 

(1) -> UNTYP := Lambda Untyped
(1)  Lambda(Untyped)
                    Type: Type

Constructors

First we can enter some variables, at the moment they are not inside a lambda-term so they can't yet be bound, but later we can put them into a lambda-term.

A numeric name is interpreted as a De Bruijn index when put inside a lambda-term, although we don't need this notation for I/O unless we are trying to avoid some ambiguity, because free and bound variables can be constructed by giving the variable name as a string. So in (4) is not yet a valid term on its own but it will be when put inside a lambda-term, when this is done it will be given the name of the bound variable rather than "0".

Internally a string name will be converted to a De Bruijn index when put inside a matching lambda-term, otherwise it will be interpreted as a free variable. 

(2) -> v1 := lambda(var("x")$Untyped)$UNTYP
(2)  "x"
                    Type: Lambda(Untyped)
(3) -> v2 := lambda(var("y")$Untyped)$UNTYP
(3)  "y"
                    Type: Lambda(Untyped)
(4) -> v3 := lambda(0)$UNTYP
(4)  "0"
                    Type: Lambda(Untyped)

This can be built up into more complex lambda terms by using compound terms (as in (5)) and the lambda-term itself (as in (6)).

Each lambda-term can only have one bound variable, if more than one bound variable is required then lambda-terms can be nested. lambda-term requires that the bound variable be given a name. 

(5) -> n1 := lambda(v1,v2)$UNTYP
(5)  "(x y)"
                    Type: Lambda(Untyped)
(6) -> n2 := lambda(n1,var("x")$Untyped)$UNTYP
(6)  "(\x.(x y))"
                    Type: Lambda(Untyped)

In (7) \verb'x' is a the bound variable and so, when the lambda-term was created, this will be converted to De Bruijn index, in (7) we call toString to see the internal representation:

In (8) we see that when entered as a numeric index the bound variable will still be displayed as a string.

In (9) and (10) we can see that the \verb'unbind' function can be used to unbind the bound variable \verb'x' that is, although \verb'x' has the same string value as the lambda term, it is treated as though it were different. We can see this because the toString output does not have a index value. In (11) we call \verb'bind' to re-bind it. 

(7) -> toString(n2)$UNTYP
(7)  "(\x.(0 y))"
                    Type: String
(8) -> n3 := lambda(v3,var("x")$Untyped)$UNTYP
(8)  "(\x.x)"
                    Type: Lambda(Untyped)
(9) -> u2 := unbind(n2)$UNTYP
(9)  "(\x.(x y))"
                    Type: Lambda(Untyped)
(10) -> toString(u2)$UNTYP
(10)  "(\x.(x y))"
                    Type: String
(11) -> toString(bind(u2))$UNTYP
(11)  "(\x.(0 y))"
                    Type: String

So we can already construct any type of lambda term, however its a bit tedious to construct complex lambda terms in this way, an easier way is to use 'parseLambda' to construct the lambda term from a string. Again we can enter variables as either alpha or numeric characters depending on whether we want to specify the index value directly or allow the code to generate it.

In (14) we can see the use of numeric terms to avoid the ambiguity caused by nested lambda-terms with the same name. 

(12) -> n4 := parseLambda("\x.\y. y x")$UNTYP
(12)  "(\x.(\y.(x y)))"
                    Type: Lambda(Untyped)
(13) -> toString(n4)$UNTYP
(13)  "(\x.(\y.(0 1)))"
                    Type: String
(14) -> n4a := parseLambda("\x.\x. 0 1")$UNTYP
(14)  "(\x.(\x'.(x x')))"
                    Type: Lambda(Untyped)
(15) -> toString(n4a)$UNTYP
(15)  "(\x.(\x.(0 1)))"
                    Type: String
(16) -> unbind(n4a)$UNTYP
(16)  "(\x.(\x'.(x x)))"
                    Type: Lambda(Untyped)

beta-substitution

The command: 'subst:(n,a,b)' substitutes 'a' for 'b' in \verb'n' as follows: 

(17) -> subst(n2,v2,v1)$UNTYP
(17)  "(\x.(x y))"
                    Type: Lambda(Untyped)
(18) -> subst(n2,v1,v2)$UNTYP
(18)  "(\x.(x x))"
                    Type: Lambda(Untyped)

Issues

I realise that Axiom/FriCAS already has a way to create anonymous functions using '+->' in a lambda-calculus sort of way. But the aim here is to represent lambda-calculus as a pure mathematical structure so that we can experiment with the properties of this structure without the messy features that are required for a practical computer language. I also need a domain structure which is related to SKI combinators and IntuitionisticLogic domain and can be coerced to and from these other domain types as demonstrated on this page.

I also realise that this is written in SPAD which is written in Lisp which is based on lambda-Calculus (perhaps it could later be optimised by having direct calls to Lisp?) Relationship to Other Domains

Relationship to Other Domains

lambda-calculus can be coerced to and from SKI combinators. For a tutorial about how to coerce to/from this algebra see below.

domain LAMBDA Lambda

SKI Combinators

for more details see:

https://www.euclideanspace.com/maths/standards/program/mycode/computation/ski/

Ski combinators were introduced by Moses Schoenfinkel and Haskell Curry with the aim of eliminating the need for variables in mathematical logic. It is equivalent to lambda calculus but it can be used for doing, without variables, anything that would require variables in other systems.

The structure is a self-modifying binary tree.

Tutorial

On this page we will be working with 'untyped' SKI combinators so we create an instance called UNTYP to simplify notation: 

(1) -> UNTYP := SKICombinators Untyped
(1)  SKICombinators(Untyped)
                    Type: Type

Constructing SKI combinators

SKI combinators consist of a binary tree structure where the leaves of the tree are either 'I', 'K' or 'S' combinators or variables.

The 'I', 'K' and 'S' combinators can be constructed by using the $I()$, $K()$ and $S()$ functions.

Variables (representing functions) can be constructed by pass this variable to a ski constructor to create a SKI term: 

(2) -> m1 := I()$UNTYP
(2)  "I"
                    Type: SKICombinators(Untyped)
(3) -> m2 := K()$UNTYP
(3)  "K"
                    Type: SKICombinators(Untyped)
(4) -> m3 := S()$UNTYP
(4)  "S"
                    Type: SKICombinators(Untyped)
(5) -> v1 := ski(var("x")$Untyped)$UNTYP
(5)  "x"
                    Type: SKICombinators(Untyped)
Compound combinator terms can be constructed by \verb'ski(node1,node2)' where
stored as a binary tree. The notation assumes association to the left,
in the absence of brackets, the term to the left binds more tightly
than the one on the right. So, in the following, we can see that:
In n2 the second term is an atom so brackets are not required.
In n3 the second term is compound so brackets are required.

(6) -> n1 := ski(m1,m2)$UNTYP
(6)  "IK"
                    Type: SKICombinators(Untyped)
(7) -> n2 := ski(n1,m3)$UNTYP
(7)  "IKS"
                    Type: SKICombinators(Untyped)
(8) -> n3 := ski(m3,n1)$UNTYP
(8)  "S(IK)"
                    Type: SKICombinators(Untyped)

In addition, to avoid having to build up this node by node, there is a quicker way to construct SKI combinators. We can construct the whole binary tree from a single string using the \verb'parseSki' constructor as follows. Again the notation assumes association to the left, in the absence of brackets, the term to the left binds more tightly than the one on the right.

When we are using parseSki and we have two variables next to each other (such as \verb'x y') then we must put a space between the variables, this is so that we can gave a variable a name consisting of multiple characters. So \verb'xy' is a single variable but \verb'x y' is two variables. All variables must start with a lower case letter. The combinators 'I', 'K', and 'S' do not need to be separated with a space since they always consist of 1 character. 

(9) -> n4 := parseSki("IKS")$UNTYP
(9)  "IKS"
                    Type: SKICombinators(Untyped)
(10) -> n5 := parseSki("S(IK)")$UNTYP
(10)  "S(IK)"
                    Type: SKICombinators(Untyped)

redux

Now that we have constructed our SKI combinator we can apply the combinators using the redux function. This allows us to apply the self-modifing binary tree.

The first combinator to investigate is 'I'. This is a do nothing combinator: 

(11) -> s1 := parseSki("Ix")$UNTYP
(11)  "I x"
                    Type: SKICombinators(Untyped)
(12) -> redux(s1)$UNTYP
x
(12)  "x"
                    Type: SKICombinators(Untyped)

The next combinator to investigate is 'K'. This removes the final variable: 

(13) -> s2 := parseSki("Kx y")$UNTYP
(13)  "K x y"
                    Type: SKICombinators(Untyped)
(14) -> redux(s2)$UNTYP
x
(14)  "x"
                    Type: SKICombinators(Untyped)

The next combinator to investigate is 'S' This applies the first two functions to the third: 

(15) -> s3 := parseSki("Sx y z")$UNTYP
(15)  "S x y z"
                    Type: SKICombinators(Untyped)
(16) -> redux(s3)$UNTYP
x z(y z)
(16)  "x z(y z)"
                    Type: SKICombinators(Untyped)

Secondary Combinators

Any calculation can be done by some combination of 'K' and 'S'. However some sequences occur frequently so it is worth assigning them special letters:

Operator What it does SKI equivalent (normal form)
'I' Identity (leave unchanged) 'I' or 'SKK' or 'SKS'
'B' Function composition 'S(KS)K'
'B' Reverse function composition  
'C' Swap functions 'S(K(SI))K'
'K' Form constant function 'K'
'S' Generalized composition 'S'
'W' Doubling or diagonalizing  

So we can see in the 3 examples below :

In 17 that 'SKKxy' is equivalent to 'xy', that is 'SKK' is identity, equivalent to I In 19 that 'S(K(SI))Kxy' is equivalent to 'yx', so "S(K(SI))K" reverses its operands. 

(17) -> redux(parseSki("SKKx y")$UNTYP)$UNTYP
K x(K x)y
x y
(17)  "x y"
                    Type: SKICombinators(Untyped)
(18) -> redux(parseSki("S(KS)x y")$UNTYP)$UNTYP
KS y(x y)
S(x y)
(18)  "S(x y)"
                    Type: SKICombinators(Untyped)
(19) -> redux(parseSki("S(K(SI))Kx y")$UNTYP)$UNTYP
K(SI)x(K x)y
Iy(Kx y)
y x
(19)  "y x"
                    Type: SKICombinators(Untyped)

SKI combinators can be coerced to and from lambda-calculus and intuitionistic logic. For a tutorial about how to coerce to/from these algebras see this page.

To Do

These are issues to think about for longer term development of this domain.

Currently this only works with variables, this means that: 

redux applied to 'SKKx y' gives 'x y'
but redux applied to 'SKK' does not give 'I'

That is, I am looking for a way to 'lift' from working in terms operators acting on variables to working in terms of operators only.

It would be good to be able to use these combinators to operate on Axiom/FriCAS functions.

I also have Axiom/FriCAS coding for lambda-caculus, as explained on this page, where there is explanation and tutorial.

domain SKICOMB SKICombinators

Logic Utility Package

The compUtil package provides utilities to convert between the computational domains: Lambda, Ski and ILogic.

Both Lambda are Ski are Turing complete and can be coerced to each other. Lambda and Ski are not equal and they are only equivalent up to beta-equivalence and beta-equivalence is undecidable so there is not a direct correspondance between the nodes in their trees. Also the names of bound variables and other such constructions may be lost in

An element of ILogic cannot be coerced to the other types. However ILogic can be used to produce a theory which can be concerted to/from the other domains using Curry-Howard isomorphism.

Tutorial

First make sure this package is exposed. 

(1) -> )expose COMPUTIL

compUtil is now explicitly exposed in frame frame1

On this page we will be working with 'untyped' variables in lambda and SKI terms so we create instances called LU and SU to simplify notation: 

(1) -> LU := Lambda Untyped
(1)  Lambda(Untyped)
                    Type: Type
(2) -> SU := SKICombinators Untyped
(2)  SKICombinators(Untyped)
                    Type: Type

SKI combinators to lambda functions

We can then create SKI combinators and convert them to lambda functions.

If the combinators don't have the required parameters then you will get a warning as follows. The code will attempt to add parameters as required but this will not work in complicated situations.

Ideally when working with 'abstract' combinatiors we need to add the required number of parameters, do the convertion then remove the parameters just added. 

(3) -> I()$SU::LU
util coerce rule SL1: Ski[I] = \v0.0
(3)  "(\v0.v0)"
                    Type: Lambda(Untyped)
(4) -> K()$SU::LU

util coerce rule \verb'SL2: Ski[K] = \v0.\v1.1' 

(4)  "(\v0.(\v1.v1))"
                    Type: Lambda(Untyped)
(5) -> S()$SU::LU

util coerce rule \verb'SL3: Ski[S] = \v0.\v1.\v2.(2 0 (1 0))' 

(5)  "(\v0.(\v1.(\v2.(v2 (v0 (v1 v0))))))"
                    Type: Lambda(Untyped)

In the following examples the combinators are provided with the required parameters. This conversion works by applying the following rules: 

rule SL1: Ski[I] = \x.0
rule SL2: Ski[K] = \x.\y.1
rule SL3: Ski[S] = \x.\y.\z.(2 0 (1 0))
rule SL4: Ski[(E1 E2)] = (Ski[E1] Ski[E2])

So here are some examples: 

(6) -> parseSki("Ia")$SU::LU
util coerce apply rule SL1 in:I a
util coerce pass unbound variable a unchanged
(6)  "a"
                    Type: Lambda(Untyped)
(7) -> parseSki("Ka b")$SU::LU
util coerce apply rule SL2 in:K a b
util coerce pass unbound variable a unchanged
(7)  "a"
                    Type: Lambda(Untyped)
(8) -> parseSki("K(a b)c")$SU::LU
util coerce apply rule SL2 in:K(a b) c
util coerce rule SL4: Ski[(a b)] = (Ski[a] Ski[b])
util coerce pass unbound variable a unchanged
util coerce pass unbound variable b unchanged
(8)  "(a b)"
                    Type: Lambda(Untyped)
(9) -> parseSki("Sa b c")$SU::LU
util coerce apply rule SL3 in:S a b c
util coerce pass unbound variable a unchanged
util coerce pass unbound variable c unchanged
util coerce pass unbound variable b unchanged
util coerce pass unbound variable c unchanged
(9)  "((a c) (b c))"
                    Type: Lambda(Untyped)
(10) -> parseSki("S(K(SI))(S(KK)I)")$SU::LU
util coerce rule SL4: Ski[(S(K(SI)) S(KK)I)] = (Ski[S(K(SI))] Ski[S(KK)I])
util coerce rule SL4: Ski[(S K(SI))] = (Ski[S] Ski[K(SI)])
util coerce rule SL3: Ski[S] = \v0.\v1.\v2.(2 0 (1 0))
util coerce rule SL4: Ski[(K SI)] = (Ski[K] Ski[SI])
util coerce rule SL2: Ski[K] = \v3.\v4.1
util coerce rule SL4: Ski[(S I)] = (Ski[S] Ski[I])
util coerce rule SL3: Ski[S] = \v5.\v6.\v7.(2 0 (1 0))
util coerce rule SL1: Ski[I] = \v8.0
util coerce rule SL4: Ski[(S(KK) I)] = (Ski[S(KK)] Ski[I])
util coerce rule SL4: Ski[(S KK)] = (Ski[S] Ski[KK])
util coerce rule SL3: Ski[S] = \v9.\v10.\v11.(2 0 (1 0))
util coerce rule SL4: Ski[(K K)] = (Ski[K] Ski[K])
util coerce rule SL2: Ski[K] = \v12.\v13.1
util coerce rule SL2: Ski[K] = \v14.\v15.1
util coerce rule SL1: Ski[I] = \v16.0
(10)
"(((\v0.(\v1.(\v2.(v2 (v0 (v1 v0)))))) ((\v3.(\v4.v4)) ((\v5.(\v6.(\v7.(v7 (v
5 (v6 v5)))))) (\v8.v8)))) (((\v9.(\v10.(\v11.(v11 (v9 (v10 v9)))))) ((\v12.(
\v13.v13)) (\v14.(\v15.v15)))) (\v16.v16)))"
                    Type: Lambda(Untyped)

lambda functions to SKI combinators

We can then create lambda functions and convert them to SKI combinators.

For a tutorial about working with SKI combinators see this page. For a tutorial about working with lambda functions see this page.

This process is known as abstraction elimination. It is done by applying the following rules until all lambda terms have been eliminated. 

rule LS1: Lam[x] => x
rule LS2: Lam[(E1 E2)] => (Lam[E1] Lam[E2])
rule LS3: Lam[\x.E] => (K Lam[E]) (if x does not occur free in E)
rule LS4: Lam[\x.x] => I
rule LS5: Lam[\x.\y.E] => Lam[\x.Lam[\y.E]] (if x occurs free in E)
rule LS6: Lam[\x.(E1 E2)] => (S Lam[\x.E1] Lam[\x.E2])

Here are some examples: 

(11) -> parseLambda("x")$LU::SU
util coerce rule LS1 applied to:x giving x
(11)  "x"
                    Type: SKICombinators(Untyped)
(12) -> parseLambda("x y")$LU::SU
util coerce rule LS2 applied to:(x y) giving (x y)
util coerce rule LS1 applied to:x giving x
util coerce rule LS1 applied to:y giving y
(12)  "x y"
                    Type: SKICombinators(Untyped)
(13) -> parseLambda("\x.1")$LU::SU
util coerce rule LS3 applied to:(\x.1) giving K 1
util coerce rule LS1 applied to:1 giving 1
(13)  "K 1"
                    Type: SKICombinators(Untyped)
(14) -> parseLambda("\x.0")$LU::SU
util coerce warning could not match any rule to:(\x.0)
(14)  "I"
                    Type: SKICombinators(Untyped)
(15) -> parseLambda("\x.\y.0 1")$LU::SU
util coerce rule LS5 applied to:(\x.(\y.(0 1))) giving \x.(\y.(0 x))
util coerce rule LS6 applied to:(\y.(0 x)) giving S \y.y \y.x
util coerce rule LS1 applied to:y giving y
util coerce rule LS4' applied to: \y.y giving I
util coerce rule LS1 applied to:x giving x
util coerce rule LS3' applied to: \y.x giving K x
util coerce rule LS5' applied to: \x.SI(Kx) giving S \x.SI \x.Kx
util coerce rule LS3' applied to: \x.SI giving K \x.S \x.I
util coerce rule LS5' applied to: \x.Kx giving S \x.K \x.x
util coerce rule LS3' applied to: \x.K giving K K
util coerce rule LS4' applied to: \x.x giving I
(15)  "S(K(SI))(S(KK)I)"
                    Type: SKICombinators(Untyped)

SKI combinators to Intuitionistic Logic

We can then create SKI combinators and convert them to intuitionistic logic.

This is known as the Curry-Howard isomorphism it uses the following rules: 

rule SI1: Ski[Kab] => a -> (b -> a)
rule SI2: Ski[Sabc] => (a -> (b -> c)) -> ((a -> b) -> (a -> c))
rule SI3: Ski[a a->b] => b

The last rule is function application (modus ponens). Here are some examples: 

(16) -> parseSki("Ia")$SU::ILogic
util coerce apply rule SI1 in:Ia
warning I does not have a parameter to act on
creating x
(16)  "((x->x)->(x->x))"
                    Type: ILogic
(17) -> parseSki("Ka b")$SU::ILogic
util coerce apply rule SI2 in:K a b
(17)  "(b->(a->b))"
                    Type: ILogic
(18) -> parseSki("K(a b)c")$SU::ILogic
util coerce apply rule SI2 in:K(a b) c
(18)  "(c->((a\/b)->c))"
                    Type: ILogic
(19) -> parseSki("Sa b c")$SU::ILogic
util coerce apply rule SI3 in:S a b c
(19)  "((c->(b->a))->((c->b)->(c->a)))"
                    Type: ILogic

package COMPUTIL compUtil

Code Generation Package

For more information about this package see: this page

Maps abstract computational structures to real-world FriCAS code.

compCode is a package in the computation framework that allows FriCAS source code to be created from the abstract structures in the framework. This is done by the following functions:

writePackage

'writePackage' creates source code for a FriCAS package from a list of lambda structures over typed variables. This is reasonably easy to do since functions in a FriCAS package have a similar structure to lambda functions.

Parameters are:

writeCategory

'writeCategory' creates source code for a FriCAS package from a list of ILogic structures. This relies on the Curry-Howard isomorphism between intuitionistic logic and types in a computation.

Parameters are:

Example

In intuitionistic logic if we know 'a' and we know 'a->b' then we can deduce b (by modus ponens) that is: 

(a /\ (a -> b) ) -> b

Curry-Howard isomorphism relates this intuitionistic logic to types in a computation so given types 'a' and 'a->b' then we can create any of these function types without using additional information (other functions or constants): 

func1:(a,a->b) -> a
func2:(a,a->b) -> (a->b)
func3:(a,a->b) -> b

func3 is more interesting since func1 and func2 can be created by passing on one of its parameters and throwing away the other.

So how can we implement this? From the original (a /\ (a -> b) ) we need to expand out to (a /\ (a -> b) /\ b) containing all factors.

By the Curry-Howard isomorphism we can coerce to the intuitionisticLogic from Lambda. This gives an isomorphism where theorems in intuitionistic logic correspond to type signatures in combinatory logic and programs in intuitionistic logic correspond to the proofs of those theorems in combinatory logic.

As an example of this in Haskell see "Djinn, a theorem prover in Haskell" [2]

see also: Philip Wadler - Theorems for free! [1]

Code Generation Package - Tutorial

First we may need to expose the reqired code such as ILOGIC and COMPCODE 

(1) -> )expose COMPCODE
(1) -> )expose ILOGIC

We can generate the source code for a FriCAS package from lambda expressions. To start we will create some typed variables and lambda terms to work with: 

(1) -> vx := var("x",proposition("String"))$Typed
(1)  "x:String"
                    Type: Typed
(2) -> vy := var("y",proposition("String"))$Typed
(2)  "y:String"
                    Type: Typed
(3) -> nx := lambda(vx)
(3)  "x"
                    Type: Lambda(Typed)
(4) -> ny := lambda(vy)
(4)  "y"
                    Type: Lambda(Typed)

Now we create some lambda expressions to be converted to source code: 

(5) -> pacEx1:Lambda Typed := lambda(nx,vx)$Lambda Typed
(5)  "(\x.x)"
                    Type: Lambda(Typed)
(6) -> pacEx2:Lambda Typed := lambda(pacEx1,vy)$Lambda Typed
(6)  "(\y.(\x.y))"
                    Type: Lambda(Typed)
(7) -> pacEx3:Lambda Typed := lambda(lambda(nx,ny),vy)$Lambda Typed
(7)  "(\y.(x y))"
                    Type: Lambda(Typed)

Now we generate the source code using the writePackage function where: 

(8) -> writePackage([pacEx1,pacEx2,pacEx3],"testComp1.spad","TESTCCP","TestCCP","Type")
                    Type: Void

When we look at the testComp1.spad file we can see the code that has been generated: 

)abbrev package TESTCCP TestCCP
TestCCP(): Exports == Implementation where
Exports ==> Type with
Implementation ==> add
fn1(x:String):String == x
fn2(y:String):String ==  x+->(y)
fn3(y:String):String ==  x(y)
@

This code may have to be tweeked by hand before it can be used.

Now we can move on to generate the source code for a FriCAS category from intuitionistic logic expressions. To start we will create some intuitionistic logic terms as examples: 

(9) -> catEx1:ILogic := implies(proposition("a"),proposition("b"))/\proposition("a")
(9)  "((a->b)/\a)"
                    Type: ILogic
(10) -> catEx2:ILogic := proposition("a")/\proposition("b")
(10)  "(a/\b)"
                    Type: ILogic

Now we generate the source code using the writeCategory function where: 

(11) -> writeCategory([catEx1,catEx2],"testComp2.spad","TESTCC","TestCC")
                    Type: Void

When we look at the testComp2.spad file we can see the code that has been generated: 

)abbrev category TESTCC TestCC
TestCC() : Category == Type with
fn1:(a->b,a) -> b
fn2:(a,b) -> a
@

In fn1 type 'b' was generated from 'a->b' and 'a' (by modus ponens). If two or more deductions were made then only the first would be used. In fn2 no additional deductions could be made, in this case the first parameter is used as the deduction.

For more details see:
[1] Philip Wadler 1989 - Theorems for free!

[2] "Djinn, a theorem prover in Haskell, for Haskell" here and here

[3] Roy Dyckhoff 1992 - Contraction-free sequent calculi for intuitionistic logic

[4] computation

[5] Tutorial for lambda calculus

[6] Tutorial for SKI calculus:

[7] Tutorial for Intuitionistic Logic

[8] Tutorial for utilities to coerce between computation domains

[9] Tutorial for FriCAS source code generation

[10] J. Lambek, P. J. Scott 1988 Introduction to Higher-Order Categorical Logic ISBN: 0521356539 This book shows the relationship between mathematical logic and category theory. Although this is not used in the current code, it suggests a promising generalisation.

[11] Peter J. Denning, 2010 Discussion of "What is computing?"

metadata block
see also:

"Propositions as Types" by Philip Wadler
Correspondence about this page

This site may have errors. Don't use for critical systems.

Copyright (c) 1998-2023 Martin John Baker - All rights reserved - privacy policy.