Dependant Types seem to be needed but we would loose type safety, so here we look for a compromise so that we can keep some degree of type safety.
This approach has a two level hierarchy:
First we construct a type:
Type V = Vector(real,3)
Then we can construct elements of that type:
a = V(3,4,5) b = V(2,6,8)
then we can do operations on these elements, such as:
a + b
This gives an extra overhead of having 2 levels of constructor but it means that we are prevented by the type system from adding a 2-dimensional vector to a 3-dimensional vector. This means we find such errors at compile-time rather than run-time.
However there are still some issues:
- Mainstream languages don't have allow instances of a class to construct an instance of an instance.
- We don't always want to do calculations in an object oriented way.
Therefore we could implement the second level of instantiation, not a true object, but as a 'fixed' object type represented by an expression.
Expression
Examples of an expression are:
- x
- x+y
- 3.14
- (2,3,5)
- sin(x)^2 + cos(y)^2
Expressions may not reduce to a single value, especially if they have symbolic values or if they represent compound types.
So an expression might contain an integer, a double (being the closest approximation to a real literal), a char, string or boolean. Or it could be an Expression containing multiple values. So a single Expression instance is a Union (Sum type), that is it holds int or double or ... but not both. If we need multiple values (Product type) then we use the Expression[] entry to build up compound types. |
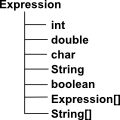 |
This appears to destroy type safety but each Expression should have a corresponding TypeExpression so that types are statically checked.
Only certain values of Expression are valid with certain types. For instance, an int value in Expression (say '42') is only valid if the TypeExpression has a value of 'int'. If an expression has a value in Expression[] then this might be a function, a record or a union. this is only determined by the Type Expression. Similarly a String value in Expression might have a type of 'string' or 'symbol'. |
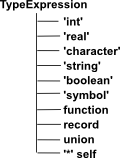 |
Self '*' allows recursively defined types such as List.
Three Layer Hierarchy
Algebraexample: Vector |
AlgebraExpression Join |
|
Typeexample: Vector(real,3) |
 |
curry (a,b)->c (a)->(b->c) |
Element |
 |
eval elt |
Model
How can we define an Eclipse model for mathematics?
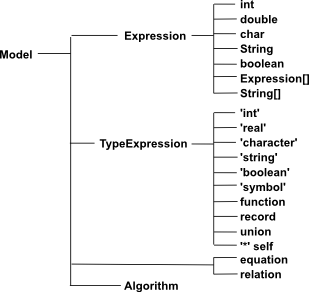
Examples
| Algebra | Field | Real | Vector | FiniteGroup (say defined as permutation group using cyclic notation) |
||
| Type | Vector(Real: Field,3: int) | FiniteGroup((1,2,3) , ( 1 3 )) | ||||
| Element | abstract | 2.5 | (2.5,3.9,7.2) | 1 |
In the case of 'vector' then it might seem more practical to define it more conventionally like this: Vector<Field> and then pass the dimension to the constructor at run-time. The dimension would then be checked each time some operation like addition is done. This could lead to some runtime overhead and some runtime errors, but because the situation is so simple, the risk is low. However if we go to something like finite groups the situation is more complicated, its not so easy to determine equality between given types of FiniteGroups (defined in some way such as cyclic notation) and our more powerful model becomes more important.
First Attempt at Dependant Type Issue
Since each algebra has multiple types and each type has multiple instances then, if we are to have any chance of implementing this as an object oriented program, then I think we will need two classes for each algebra, one for the type, and another for the instance. Here I have implemented the second as an inner class of the first. This is just pseudo code to suggest the approximate form. |
interface Field {
Field add(Field a, Field b)
Field multiply(Field a, Field b)
// ... inverses and so on
}
class Vector {
Field field; // field and dimension are state variables for algebra type
Int dimension;
Vector(Field f, Int d) { //type constructor
field=f;dimension=d;
}
class VectorInstance extends Expression {
Array<Field>(dimension) instance; // state varables for instance
VectorInstance(Array<Field>(dimension) i){intance=i}
}
// instance value constructor
VectorInstance newInstance(Array<Field>(dimension) i) {
return new VectorInstance(i)
}
VectorInstance add(VectorInstance a, VectorInstance b) {
return[for x in a, y in b yield field.add(x,y)]
// I realise java does not support list comprehensions but
// this is pseudo code to save space
}
} |