Maths - Nerve

Nerve of a Category

The nerve N(C) of a category C is a simplicial set constructed from the objects and morphisms of C.

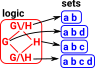
Nerve Complex

The nerve complex of a set family is an abstract complex that records the pattern of intersections between the sets in the family

The points of the simplicial set correspond to the one element sets in the open cover: {A}, {B},{C} ,{D},{E},{F}.

The edges of the simplicial set correspond to intersections of sets (two element sets) in the open cover. {A,B}, {A,C}, {B,C}, {C,D}, {D,E}, {E,F}, {B,F}.

If the intersection includes 3 sets then the simplex is a (filled in) triangle: {A,B,C}

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Here we take 3 spaces A,B and C. Then we generate all possible unions and intersections.

	combinatorial ------------ space	simplicial complex	logic
Here is a simpler diagram
Can we be sure if {a,b} is connected? contractible?
How do we treat the situation where {a,b} = {b}
What about degenerate points?

 

 

 

 

 

 

 

 

 

EuclideanSpace

home

Where Are You

This is one of a series of pages about topology, these pages start here.

See these pages for information about CW complexes and simplicial set.

Prerequisites

• Topology
• CW complexes and simplicial set.

Topological Space and Simplicial Sets (Geometric Realisation)

Topological spaces have some nice properties, they have the concept of nearness in the most general way. However topological spaces have some quite stringent requirements, geometric realisation gives use a way to embed any CW complexes or simplicial set as a topological space.

A first thought for how to embed simplicial sets in topological spaces might be to equate each simplex with an open set, unfortunately this won't work for the following reasons:

• Every union of simplices in a CW complex is not a simplex but unions of open sets must be open sets.
• Every pair of simplices don't necessarily have an intersection.

There is a way to canonically get a topological space from a simplicial complex, this requires a much higher dimensional space so its not very intuitive. For instance, to encode a graph (2D complex), each vertex in the graph needs to have its own dimension in the topological space.

Here we want to encode a complex with two points and a line. We embed this in 2 dimensional Euclidean space (and therefore topological space).

Each of the points is now a vector in its own dimension, these are [1,0] and [0,1] and they are the basis vectors. The line is a straight line between these basis vectors, parameterised by t like this { (1-t)*[1,0]+t*[0,1] | t[0,1] }.

A more complex graph gives a lot more dimensions which makes visualising the topological space harder.

For more information about geometric realisation see the page here.