This is an example for the page about sheaves which is here.
Example - Simplicial ComplexMore about simplicial complexes on this page. A simplicial complex can define a space, however this space is completely different from the topological space of the sheaf. |
Example - GraphI think we can see the sheaf idea more clearly if we first restrict ourselves to the simpler case of a graph. More about graph theory on this page and from a category theory point of view on this page. |
|
| If we were coding a graph structure in a computer language we would probably have a set of edges (E) and a set of vertices (V). Each edge has two pointers into the vertices set. One for the source(s) and one for the target(t). |
|
So this is what it looks like in set, but for a sheaf we need a map out of a topology-like structure. So what does the topology look like? hX = homC(_,X) : Grf op-> Set note that in Grf op then s and t are not set theoretic functions (not constructed from surjective an injective maps) but are the reverse of this. |
|
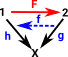
It is easier to see this contravarience from this diagram. If 'F' is given we can derive 'h' from 'g' by composing with 'F' but we can't derive 'g' from 'h'. So if we want to get the usual functions in set we need to start with Grfop |
 |
|
So now we can show the sheaf as a contravarient functor and hopefully get a better feel for its inner workings. Here Cop is a category with two objects E (for edge) and V (for vertex) also two arrows s (blue for source) and t (red for target). This allows us to build a structure on top of set where the diagram on the right commutes. We can therefore build up complex graphs from individual vertices and edges. |
 |
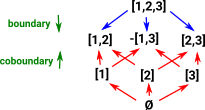
Example - Simplical Complexes
In the graph example above I think we can start to see the structure but, in that case, the topology is so simple that we might not see all the interactions. So it might be worth looking at a more complicated case.
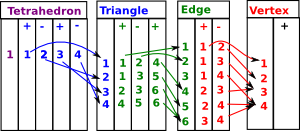
Here we extend from verticies and edges to include triangles and tetrahedrons up to any dimension. There are various ways to encode these structures. Here each dimension is coded in terms of the dimension below it, this is known as a delta complex. In terms of topology this gives a sense of nearness since a vertex is nearer to the edge than to the triangle. |