Equalities, such as 1+1=2, that contain only literal values will usually normalise to a single value on each side of the equation like 2=2 which can either be constructed (proven) or not.
The interesting cases tend to be equations with variables such as 'x+0=x'.
| However, if we enter such an equation we will get an error: 'No such variable x' |
|
To represent variables we need to use a function from the type of the variable to the equality type: |
|
So this is a dependent type.
As with alpha conversion in lambda calculus the name of the variable can be changed like this:. |
|
These equalities, such as'x+0=x', with a variable need to be true for all values of the variable. That is, there is an implied for all
quantifier. If we need an exists
quantifier then we need to investigate 'decidable types on this page.
Variables
We can represent variables in an equation by using dependent types, like this:
plusZeroRightNeutral: (x:Nat) -> (x = plus x Z)
So this generates a family of types:
- 0 = plus 0 Z
- 1 = plus 1 Z
- 2 = plus 2 Z
- ...
To prove it we must be able to construct for every value of x (it must be total).
Examples
To prove equalities with variables we need to prove it for every value of the variable.
| If the variable is a Boolean then it is easy to do for all possible values: |
|
| If the variable is a Nat then we need to use induction/recursion: |
|
So this generates a family of types:
- 0 = plus 0 Z
- 1 = plus 1 Z
- 2 = plus 2 Z
- ...
To prove it we must be able to construct for every value of x (it must be total).
Here are some more examples, the following will compile:
test0 : x=plus Z x test0 = Refl test1 : x=plus Z x -> x=plus Z x test1 p = p -- does not normalise --test2 : x=plus x Z --test2 = Refl test3 : x=plus x Z -> x=plus x Z test3 p = p |
Equality Type Families
| A type family like this: |
|
|
| is not equal to this type family: |
|
even though one implies the other one. So, given a proof of one can we get a proof of the other one? In algebra, if we do the same thing to both sides of an equation (in this case increment) then the equation is still valid.
| In Idris we can generalise like this: Where P x is a property of x. P : a -> Type |
|
To use this in our proofs there is the following function in the prelude:
||| Perform substitution in a term according to some equality.
replace : {a:_} -> {x:_} -> {y:_} -> {P : a -> Type} -> x = y -> P x -> P y
replace Refl prf = prf |
Equality Parameters
In this case we are considering parameters of the form x=y
We can think of the parameters of a proof function as being analogous to the antecedent or context of a proof. When a proposition is true but we can't constuct it directly with Refl the compiler needs some help, one way to help the compiler is to give more information through extra parameters.
testP1 : 1=1 -> 1+1=2 testP1 Refl = Refl |
Here the parameter 1=1 is not required and does not do anything. It can always be constructed with Refl. |
plusxZ2 : x=plus x Z -> x=plus x Z plusxZ2 p = p |
Here is a trivial example which says, given a proof of x=plus x Z then x=plus x Z. |
plusxZ2 Refl = Refl -- gives error |
We can't prove the above like this though. |
incBothSides : x = y -> S x = S y incBothSides Refl = Refl |
If we have a proof of x=y then we can get a proof of S x = S y This is a specific example of a more general idea cong (congruence) defined in libs/prelude/Prelude/Basics.idr Why does this work, but the example above does not? |
If an equality is provable but the above methods still don't allow Idris to complete the proof then we may need to substitute a variable using the Idris replace or rewrite constructions. This is described on this page.
incx : (x : Nat) -> x = (plus x Z) -> S x = S (plus x Z) incx x p = rewrite p in Refl |
rewrites x to plus x 0 in S x = S (plus x Z) |
Properties
| In set theory a property can be given by a function from Set to Bool. For instace: the property of being an even number can be represented like this: |  |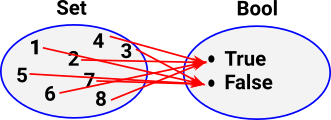
| Since we are using constructive logic we represent properties as a function into a type (in this case an equation). |  |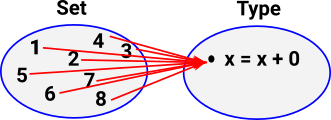
So, in Idris, this is not intended for a property like this: which can't be proved for all values of n (that is, it generates a type that can't be constructed, using Refl, for all values of n). |
p1: Nat -> Type p1 n = (n=2) |
|
Whereas a property like this: can be proved for all values of n |
p2: Nat -> Type p2 n = (n=n+0) |
| So 'p1' can be contructed at 2 but when we try to construct at 3 we get an error as expected: | *proof> the (p1 2) Refl
Refl : 2 = 2
*proof> the (p1 3) Refl
(input):1:1-15:When checking argument value to function Prelude.Basics.the:
Type mismatch between
x = x (Type of Refl)
and
p1 3 (Expected type)
Specifically:
Type mismatch between
1
and
0
|
| As expected we can construct 'p2' at any value. However this needs to be proved and, for this we need Replace or Rewrite. | *proof> the (p2 2) Refl Refl : 2 = 2 *proof> the (p2 3) Refl Refl : 3 = 3 *proof> |
Equality of Equalities
I tried making an equality between two equalities |
eq2 : ((x : Nat) -> x = plus x 0) = ((y : Nat) -> y = plus y 0) eq2 = Refl |
but that does not work: |
26 | eq2 = Refl
| ~~~~
Universe inconsistency.
Working on: ./equality.idr.x3
Old domain: (5,5)
New domain: (5,4)
|
