EndofunctorsWe have already described (on this page) a Transformation as a mapping from the points in a vector space back to itself. |
|
| A transform maps every point in space to a (possibly) different point. This type of function, that maps something back to itself, is known as an 'endofunction' | 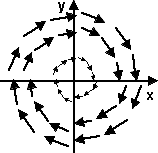 |
There is a difference, in concept, between the two diagrams above. The top diagram is a mapping between a whole algebra (vector space) back to itself. The bottom diagram shows a mapping between elements of an algebra (points) back to those elements.
When we are dealing with functions between whole algebras (functors) like this, we can use a branch of mathematics known as category theory. This allows us to discover some general properties of transformations.
Natural Transformations
This concept of an endofunction is very powerful because it allows us to compose it indefinitely, that is, we can apply it over and over again and each time we will get a transformation as the result. In mathematical terminology: it is 'closed'.
So what types of transformation are there? The first is the identity ('Id' or '1'), which is the same as doing nothing, this may not seem very useful but it is an important concept in the higher order algebra of vector space transformations. It is like multiplying by one.
There are also two 'natural transformations', these are mappings between transformations that obey certain axioms, these two natural transformations are:
- unit η: 1 -> T
- multiplication µ: T² -> T
Together the endofunctor and natural transformations form a monad which then allows us to define a higher order algebra of transformations (in fact several algebras).
The first natural transformation 'unit' denoted by the symbol 'η' (the Greek lower case eta) is a mapping from the identity to a transform: 1 -> T. When we apply this to a point 'p' then we get: p -> T p. So unit just introduces a transformation.
The second natural transformation 'multiplication' denoted by the symbol 'µ' (the Greek lower case mu) is a mapping from a transform applied twice (T²) to a single transform. This is just an encoding of the 'closure' principle, that is, if we apply a transformation and then apply another transformation then that is equivalent to some single transformation.
Properties of Vector Space Transformations
So far we have not said anything about what type of transformation that we are discussing (Rotation, Scaling, Reflection, Translate, Shear and so on), we don't need to, these are completely general and apply to all of these.
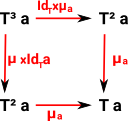
For this endofunctor and natural transformations to form a monad it must obey some axioms which expressed in category theory diagrams are:
| associative square: | unit triangles: |
 |
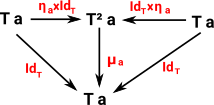 |
This looks complicated, if you are not used to category theory diagrams, but it is just encoding two simple principles:
- Transformations are associative. That is, if we are applying 3 transformations A, B and C, in that order. We can combine A and B first and the combine with C or B and C first and the combine with A. Note: we are not changing the order here because, as we know, the order of applying transforms is important.
- Composing the unit with T, in either order, gives T.
Since these axioms apply to transformations, we have a valid monad.
Higher order Algebras
From this monad we can construct a whole category of higher order algebras with two extremes:
|
 |
Eilenberg-Moore Algebra
If 'A' and 'B' are objects in the vector space category, that is, points and 'T' is a transform on those points. Then the Eilenberg-Moore algebra for vector space has:
- objects: T A
 A
A - arrows: A->B
So objects in this algebra are the transformations, rather than the underlying points or vectors. The arrows allow us to combine them, for instance, we might multiply square matrices or quaternions to calculate the result of composition of two transformations.
Kleisli Algebra
If 'A' and 'B' are objects in the vector space category, that is points and 'T' is a transform on those points. Then the Kleisli algebra for vector space has:
- objects: A
- arrows: A->T B
So objects in this algebra are the underlying points or vectors. The arrows are now more complicated, we might multiply the matrix by a vector or quaternion sandwich product to calculate the result of transformations on actual points.
Types of Transformation
