This is discussed when we discuss polar form and Euler's equation on this page.
| z plane | w plane | |
|---|---|---|
 |
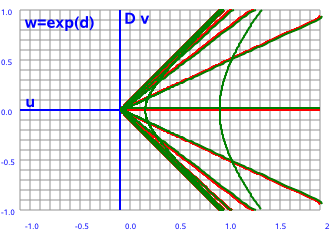
--> w=ez |
 |
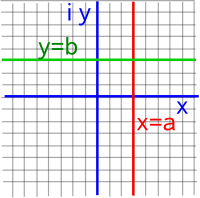
Let the components of the input and output planes be:
z = x + D y and w = u + D v
In this case w = ez
so:
w = e(x + D y)
by the rules of exponents:
w = exeD y
How do we evaluate this? We can use the hyperbolic version of Euler's equation which gives:
w = ex(cosh(y) + D sinh(y))
More about hyperbolic trig functions here.
so the u and v components are:
u = excosh(y)
v = exsinh(y)
Derivation using Infinite Series
We can calculate the exponent using the series:
| e(z) = |
|
|
Where:
- z = double number
- n= integer
- e = 2.71828
We have to be careful with quaternions because they are not in general commutative. I think the above series applies but I'm not absolutely sure.
We now need to plug in a value for (z)n which we have calculated on this page.
So substituting in our expression for the exponent gives:
| e(x + D y) = |
|
|
|
where:
| k | (-D)k | k! |
|---|---|---|
| 0 | 1 | 0 |
| 1 | -D | 1 |
| 2 | 1 | 2 |
| 3 | -D | 6 |
| 4 | 1 | 24 |
So (-D)k cycles round even terms have the dimension of -D and even terms have the scalar dimension.
Derivation of Double Number equivalent of Euler's equation
In order to express this in terms of sin and cos we need to know the series for other functions (introduced on this page).
| sin(x) | x - x3/3! + x5/5! ... +(-1)rx2r+1/(2r+1)! | all values of x |
| cos(x) | 1 - x2/2! + x4/4! ... +(-1)rx2r/(2r)! | all values of x |
| ln(1+x) | x - x2/2! + x3/3! ... +(-1)r+1xr/(r)! | -1 < x <= 1 |
| exp(x) | 1 + x1/1! + x2/2! + x3/3! ... + xr/(r)! | all values of x |
| exp(-x) | 1 - x1/1! + x2/2! - x3/3! ... | all values of x |
| e | 1 + 1/1! + 2/2! + 3/3! | =2.718281828 |
| sinh(x) | x + x3/3! + x5/5! ... +x2r+1/(2r+1)! | all values of x |
| cosh(x) | 1 + x2/2! + x4/4! ... +x2r/(2r)! | all values of x |
We start with the series:
exp(D y) = 1 + (D y)1/1! + (D y)2/2! + (D y)3/3!+ (D y)4/4! + (D y)5/5! + …
So if all dimensions square to positive then:
(D y)2 = y2 = positive scalar
so substituting gives:
exp(D y)= 1 + (D y) +y2/2! + D y3/3! + y4/4! + D y5/5! + …
splitting up into real and imaginary parts gives:
exp(D y) = 1 + y2/2! + y4/4! +…+ i( y + y3/3! + y5/5!! + …)
exp(D y) = cosh(y) + D sinh(y)


