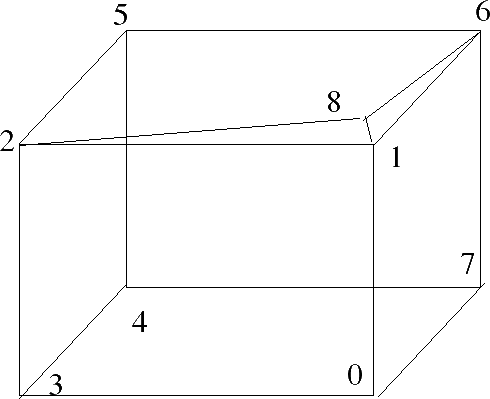
In order to show an example of mesh reduction using the Garland-Heckbert method, have chosen the above mesh. I am cheating a bit because the top face is not quite in one plane, but the error is not much and I want to keep the arithmetic simple. Assume we want to reduce the number of vertices from 9 to 8, there is an obvious candidate since two of the vertices are very close together, this should make it easier to check if the method has chosen the result we expect.
So the vertices have the following positions:
| vertex number | x coordinate | y coordinate | z coordinate |
| 0 | 1.0 | -1.0 | 1.0 |
| 1 | 1.0 | 1.0 | 1.0 |
| 2 | -1.0 | 1.0 | 1.0 |
| 3 | -1.0 | -1.0 | 1.0 |
| 4 | -1.0 | -1.0 | -1.0 |
| 5 | -1.0 | 1.0 | -1.0 |
| 6 | 1.0 | 1.0 | -1.0 |
| 7 | 1.0 | -1.0 | -1.0 |
| 8 | 0.9 | 0.8 | 0.9 |
| front face | 0,1,2,3 |
| back face | 4,5,6,7 |
| right face | 7,6,1,0 |
| left face | 3,2,5,4 |
| top face | 8,6,5,2 |
| bottom face | 3,4,7,0 |
| topRight triangle | 1,6,8 |
| topFrom triangle | 1,8,2 |
We also need to know the normals at the vertices and these are as follows:
(Note: we need per vertex normals, if we have per face normals these must be converted to per vertex normals first).
| normal number | x coordinate | y coordinate | z coordinate |
| 0 | 0.577 | -0.577 | 0.577 |
| 1 | 0.577 | 0.577 | 0.577 |
| 2 | -0.577 | 0.577 | 0.577 |
| 3 | -0.577 | -0.577 | 0.577 |
| 4 | -0.577 | -0.577 | -0.577 |
| 5 | -0.577 | 0.577 | -0.577 |
| 6 | 0.577 | 0.577 | -0.577 |
| 7 | 0.577 | -0.577 | -0.577 |
| 8 | 0.577 | 0.577 | 0.577 |
The parameters a,b,c and d are calculated as follows:
| vertex number | a= n.x | b= n.y | c= n.z | d= -(p dot n) |
| 0 | 0.577 | -0.577 | 0.577 | -1.731 |
| 1 | 0.577 | 0.577 | 0.577 | -1.731 |
| 2 | -0.577 | 0.577 | 0.577 | -1.731 |
| 3 | -0.577 | -0.577 | 0.577 | -1.731 |
| 4 | -0.577 | -0.577 | -0.577 | -1.731 |
| 5 | -0.577 | 0.577 | -0.577 | -1.731 |
| 6 | 0.577 | 0.577 | -0.577 | -1.731 |
| 7 | 0.577 | -0.577 | -0.577 | -1.731 |
| 8 | 0.577 | 0.577 | 0.577 | -1.5 |
So the Q matrices are:
Q at vertex 0:
| 0.333 | -0.333 | 0.333 | -1 |
| -0.333 | 0.333 | -0.333 | 1 |
| 0.333 | -0.333 | 0.333 | -1 |
| -1 | 1 | -1 | 3 |
Q at vertex 1:
| 0.333 | 0.333 | 0.333 | -1 |
| 0.333 | 0.333 | 0.333 | -1 |
| 0.333 | 0.333 | 0.333 | -1 |
| -1 | -1 | -1 | 3 |
Q at vertex 2:
| 0.333 | -0.333 | -0.333 | 1 |
| -0.333 | 0.333 | 0.333 | -1 |
| -0.333 | 0.333 | 0.333 | -1 |
| 1 | -1 | -1 | 3 |
Q at vertex 3:
| 0.333 | 0.333 | -0.333 | 1 |
| 0.333 | 0.333 | -0.333 | 1 |
| -0.333 | -0.333 | 0.333 | -1 |
| 1 | 1 | -1 | 3 |
Q at vertex 4:
| 0.333 | 0.333 | 0.333 | 1 |
| 0.333 | 0.333 | 0.333 | 1 |
| 0.333 | 0.333 | 0.333 | 1 |
| 1 | 1 | 1 | 3 |
Q at vertex 5:
| 0.333 | -0.333 | 0.333 | 1 |
| -0.333 | 0.333 | -0.333 | -1 |
| 0.333 | -0.333 | 0.333 | 1 |
| 1 | -1 | 1 | 3 |
Q at vertex 6:
| 0.333 | 0.333 | -0.333 | -1 |
| 0.333 | 0.333 | -0.333 | -1 |
| -0.333 | -0.333 | 0.333 | 1 |
| -1 | -1 | 1 | 3 |
Q at vertex 7:
| 0.333 | -0.333 | -0.333 | -1 |
| -0.333 | 0.333 | 0.333 | 1 |
| -0.333 | 0.333 | 0.333 | 1 |
| -1 | 1 | 1 | 3 |
Q at vertex 8:
| 0.333 | 0.333 | 0.333 | -0.865 |
| 0.333 | 0.333 | 0.333 | -0.865 |
| 0.333 | 0.333 | 0.333 | -0.865 |
| -0.865 | -0.865 | -0.865 | 2.25 |
We can now calculate any error by using the formula:
vt [Q] v
For instance, if we take Q at vertex 0, and we use the position of vertex 0 unchanged we should get zero error:
error =
|
|
|
|
|
error = 0 as required because we have not collapsed any edges yet.
Now we need to identify all the edges and try each one in turn, we can get the edges from the index table as follows:
| front face | 0 to 1 |
| back face | 4 to 5 |
| right face | 7 to 6 |
| left face | 3 to 2 2 to 5 5 to 4 4 to 3 |
| top face | 8 to 6 |
| bottom face | 3 to 4 4 to 7 7 to 0 0 to 3 |
| topRight triangle | 1 to 6 |
| topFrom triangle | 1 to 8 8 to 2 2 to 1 |
we can remove duplicates, for instance 0 to 1 is the same as 1 to 0, so this results in the following table of 15 edges:
0 to 1
0 to 3
0 to 7
1 to 2
1 to 6
1 to 8
2 to 3
2 to 5
2 to 8
3 to 4
4 to 5
4 to 7
5 to 6
6 to 7
6 to 8
We can now try collapsing each of these in turn, as an example lets collapse
the first of these (0 to 1). We well merge vertex 0 and vertex 1 to a common
vertex at their mid-point (1,0,1).
The error at vertex 0 =
|
|
|
|
|
error at vertex 0 =-0.333-0.333+1 = 0.333
The error at vertex 1 =
|
|
|
|
|
error at vertex 1 =-0.333-0.333+1 = 0.333
Therefore the total error metric when collapsing vertex 0 and vertex 1 is 0.333 + 0.333 = 0.666.
However there is an easier way to do this calculation, instead of calculating each vertex separately as above, we can add the [Q] matrix for vertex 0 and vertex 1 and then do the calculation once, this gives:
Total error =
|
|
|
|
|
Total error =-0.666-0.666+2 = 0.666
Which, as expected, is the same as the error when calculated individually.
Now we can try collapsing vertex 1 and vertex 8 as, from looking at the diagram, this is the solution we expect to produce the least distortion. We will collapse these to a common vertex at their mid-point (1.9/2,1.8/2,1.9/2) which is: (0.95 , 0.9 , 0.95)
Total error =
|
|
|
|
|
Total error =-0.00019-0.00018-0.00019+0.028 = 0.02744
As expected this is a much lower error, therefore this edge collapse will be chosen.